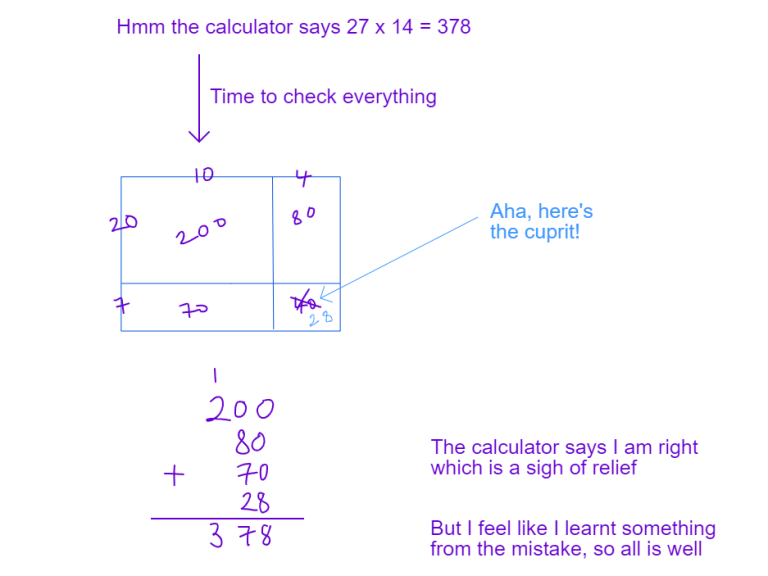
How to teach method selection by articulating internal monologue to pupils
We’ve all encountered pupils who stare at test questions blankly despite having a gut feeling on what to do. When pupils encounter a novel question on an exam, the very first emotions and thoughts they have might be something like this internal monologue: What is this question?Where do I begin?How do I decode what this…