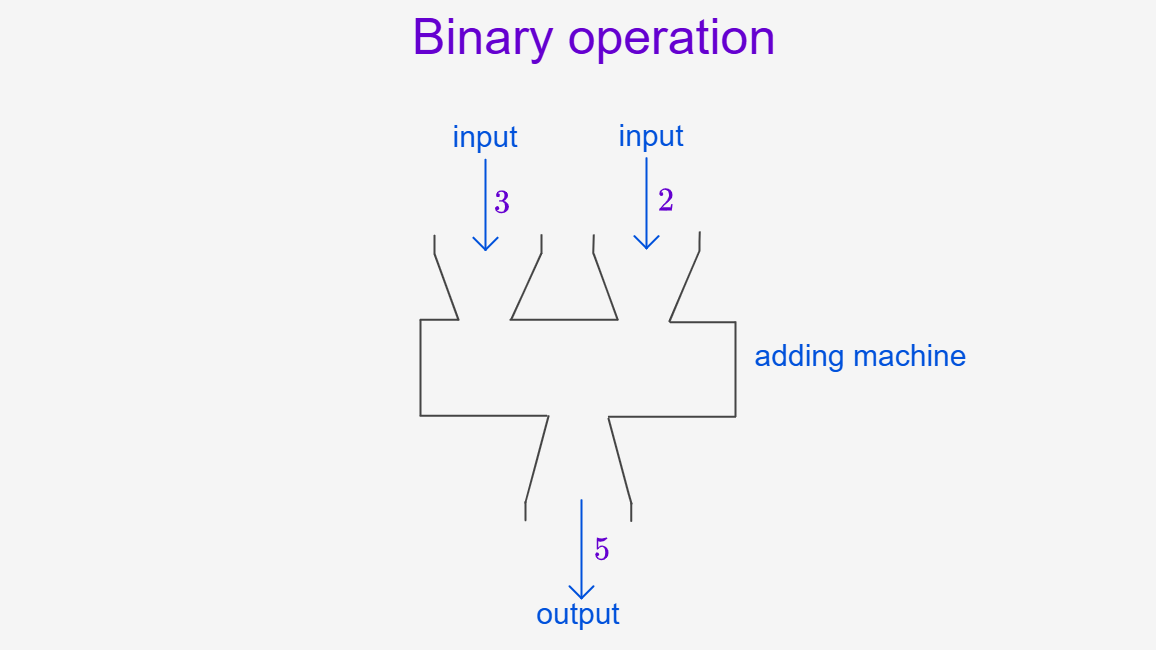
Calculators and A Christmas Carol: What the Past Teaches Us About Arithmetic
It was Christmas Eve. Bob Cratchit, hunched over his ledger in the dim light of the counting house, had more to contend with than the tyranny of Ebenezer Scrooge. There was another, quieter brutality woven into his working day—one so familiar it barely registered as a problem at all. Non-decimal currency and mixed-base arithmetic. All…