Maths Conference Sheffield (Penistone) #MathsConf19
This blog post is a write up of my sixth maths conference. #MathsConf19 was held at Penistone Grammar School near Sheffield on 22 June 2019. Run by La Salle Education, the conferences are attended by around 400 maths teachers, trainers, publishers, suppliers, academics, tutors and others involved in maths education.
TLDR ; Both real and virtual double sided counters are very versatile, the term radius is a relatively new word to the circle party. Just a few alternative methods for constructions brings the topic alive.

Pre-conference Friday night socialising
The Friday night pre-conference drinks are an invaluable opportunity for informal CPD in itself. Teachers have so many things they want to share and bounce their thoughts off others. This is the part I enjoy so much as a one man band online maths tutoring business who doesn’t get the opportunity to do much of this in person. Twitter is useful for these things but there really is no substitute to meeting in person.
I got to check in with teachers with the new A Levels for example and how teaching the first full first cohort has been. I was so impressed to meet a couple of teachers who teach everything from further A level maths to Year 7 students, from top to bottom sets. A lot of skill and versatility is needed for this which I need as well as a tutor. I am looking to teach further maths in the future so I asked some questions on the various modules for that.
Some of us were also doing maths games and puzzles. I was playing Albert’s insomnia bought in by Drew Foster. A game using mental maths and the order of operations. The beer, chatter, games and socialising continued through the evening. Unlike Bristol I took an early night after the bar closed this time. Thankfully there was no Atul’s insomnia after playing Albert’s insomnia and I was in good spirits for the following day of conferencing.
Introduction, twitter and a MacMillan award
La Salle CEO Mark McCourt kicked things off with an introduction to the maths conference. AQA maths head Andrew Taylor also gave a short talk with a “guess the year this question was set” slides showing how certain stylistic elements of questions go in an out of fashion from the 1940s to date. Mark also mentioned that there are about 300,000 maths teachers in the country and encouraged us to tweet about the event so others can get involved with the network and get out to know each other. I couldn’t agree more on the immense power gained from meeting and learning from other teachers. La Salle truly excel at creating this community; online and in person through these events. And you really can’t go wrong if the entire conference title is a hashtag itself!
Mark was pleasantly surprised by an announcement from the audience to receive the 2019 Douglas MacMillan award. All arranged and nominated for by Julia Smith. He always doubles the amount (with some generous rounding up) raised on the day from raffle ticket sales. Mark also has a new book out “Teaching for Mastery” which I really look forward to getting into. I’ve been to three of his full Complete Maths CPD days and continue to learn from his vast understanding of maths teaching.
Speed dating and some new ideas for teaching
Next up was speed dating, 4 ‘dates’ where each delegate gets 120 seconds to share their favourite teaching idea with another delegate. 120 seconds to share all my life’s knowledge on maths teaching and my greatest hits of ideas. This was going to be pretty difficult I thought. Coming out of it I learnt a lot from these dates about maths teaching; from goalless problem solving to a highly atomised approach in teaching some topics. I talked mainly about ‘backwards fading in example-problem pairs’ and the ‘pretest effect’ that I have been trialling out with some good success.
Workshop 1 : Double sided counters
This workshop was delivered by Jonathan Hall aka mathsbot. He has created a very rich resource of online manipulatives that I very highly recommend using. Double sided counters have been late to this manipulatives party for me as I still haven’t started using these with tutees. So this workshop would serve as the perfect intro to using them.

It was certainly a lot more than just an intro. Jonathan showed how this simple and one of the cheapest manipulatives can be used to explain numbers, probability, algebra and proof. Each delegate had their own set of manipulatives to play with. To start off with we were given a hotel problem with 12 closed doors to try out in our heads. It was apparent very quickly that this would be pretty hard to do mentally. As soon as the counters came in, it was easy to solve the problem with the yellow side as a ‘door open’ and red as ‘door closed’.
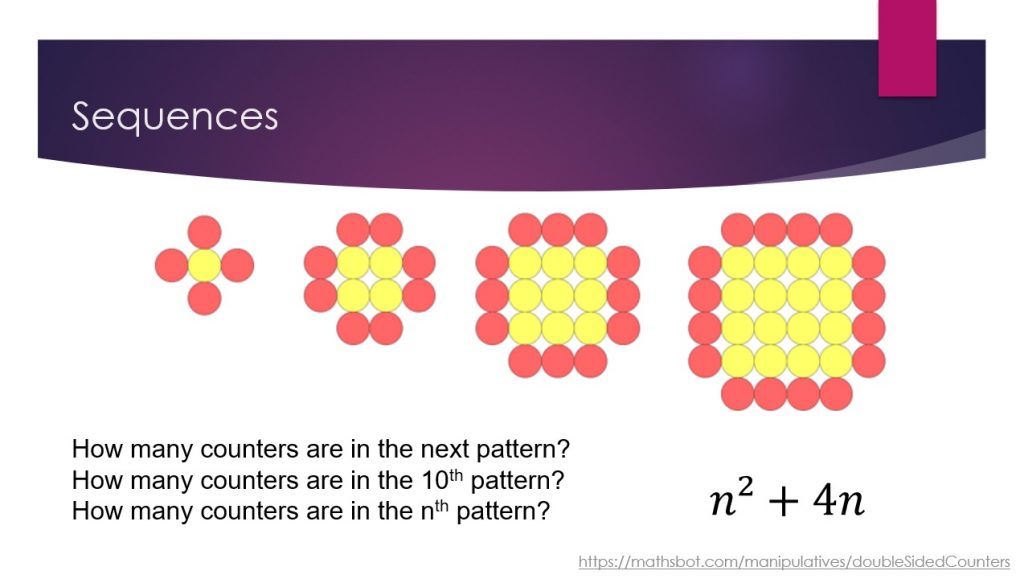
We then looked at sequences. Now I have seen these on 13+ papers a lot in picture form but there really is something else about having the actual counters in physical form and to actually build the patterns with your hands. There is something satisfying about the process of building the patterns by hand and there is no doubt this very act leads to richer understanding. We looked at a couple of sequence examples and while both examples were for quadratic sequences, the counters work very well with linear sequences as well. We were then shown some great examples of visual proof and probability questions using Venn diagrams. Everyone had an A4 sheet in which to make a Venn diagram and place the counters. Each application eventually leading to a generalised form where a total of n counters can be used. Probability being finished off by looking at a Simpson’s Paradox example case.
I was really impressed to see the counters being used for factorisation and finding the mean. In this example we had three separate groups of red and yellow counters (first row on image) then redistribute it all to get three identical rows of 2 yellows and 3 reds in each row, i.e 3(2y + 3r). The last row in the image showing elegantly how the mean is simply two yellows and three reds 2y + 3.

The presentation wrapped up showing the many uses of double sided counters. These being; Directed number, Ratio, Sequences and nth term, Proof, Averages, Collecting like terms, Factorising, Venn Diagrams, Probability, Tree Diagrams, Factors, Multiples and Primes, Square and Triangle numbers, Long Division and Modelling Problems.
I’ve already got myself a set of the counters and can’t wait to use these in my teaching.
Workshop 2 : Ratio and Proportion
The next talk was by David McEwan who is the Curriculum manager of Maths at AQA. Ratio, proportion, scaling, fractions, percentages are all of course linked topics. #MathsConf18 gave me a real appreciation of the idea of ‘scaling from unity’ so I was really looking forward to this particular workshop. Each one of us had a list of specification extracts and exam questions to accompany the workshop too.
We kicked things off by an open ended discussion on how one could define ratio (see image).

David also mentioned that ratio and proportion appears in some form or other mostly on Foundation or Higher-Foundation content. Analysing the June 2018 series he mentioned that ratio and proportion questions appear almost at the start of the paper and are evenly distributed towards almost the end. And the proportion of proportion questions? Roughly 25% in Foundation and 20% in Higher. The pun here is unavoidable and bought some chuckles around the room.
David showed the equivalence of fractions with ratios leading on to equality of ratios. Finally linking it all up with a really neat cross multiplication method suitable for all ratio-equivalence calculations.
Using bar modelling as well each percentage problem could be solved using this cross multiplication technique once the problem was set up the right way. Find the percentage, finding the number, percentage changes, reverse percentages could all be done using the bar model. I really liked the idea of going for one consistent representation and following it through.
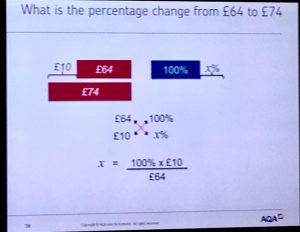
We were also shown some slides to remind us that an introduction to trigonometry is all about ratios as well and that students can essentially be introduced to trigonometry at earlier ages when introduced to right angled similar triangles. Also discussed were ratio tables showing the conversion factors for area and volume scaling and a few other concepts that showed the same thread of proportional relationships. It was really good to get such a clear reminder of this.
Workshop 3 : The Evolution of Vocabulary in Maths Education
Next up was Jo Morgan with a talk dedicated to the use of words in maths and how words change, evolve or fade out of use through time.
Words change in general over time because..
- They become obsolete (e.g ‘cassette’)
- Go out of fashion (‘groovy’ or that 90s word ‘naff’)
- They get superseded by newer ways of speaking (‘telephone’ becomes just ‘phone’)
I was very relieved to hear that “thrice” was once indeed a word. I used it when I lived in India and other countries. I stopped using the word in Year 11 when I arrived in the UK as my classmates told me that no such word exists. It must have been faded out here in the UK by that time. And apparently “twice” is on its way out now too. Being gradually replaced by “two times”. The words ‘Evenly even’ (divisible by 2 and then 2 again) and ‘evenly odd’ (divisible by 2 just the once) were also mentioned.

Jo then moved on to use of some words in the context of solving and simplifying equations. Transposition: “The act of transferring something to a different place.†and ‘concinnation‘ (simplifying in an equation) make a regular appearance. And so do terms such as ‘destroying‘, ‘clearing the fractions‘ and a verb in its own right ‘to vinculate‘.
The word ‘concinnation’ made me think of the word ‘concatenate‘ (link things together in a chain or series) that I vaguely remember using in computing. The ‘concatenate’ command is used to stitch up two or more files into one big one using the MS DOS command prompt.
On to circle geometry next. It is hard to believe now but the word radius is one of the youngest words to be used in circles and has only joined the circles party relatively recently. Mathematicians managed for a very long time without the word and using ‘semi-diameter‘ was enough. The earliest reference to radius as a mathematical term in English is Hobbes writing in 1656.
After that we got into some quadrilateral language. Rhombus “So called from the Greek word Rhombos, which signifies the Fish called a Turbot, and the Quarrels of Glass in a Window.” Rhomboids was also mentioned and discussed as what we call the modern parallelogram. And interestingly oblong is the old word used for a rectangle. The new oblong is a lot different to the old one in that way.
Jo finished off the workshop with a look at Welsh mathematician Robert Recorde‘s contribution to maths. His book The Grounde of Artes was written with a lovely tutor and student narrative with Recorde doing some tutoring to his imaginary student and the student responding back. Encouraging the scholar with “well said”. Good tutoring practice has remained unchanged all these centuries then!

One cannot mention Robert Recorde without referring to his most well known contribution, the use of the equals sign = After a little training on how to translate old English we were given the original text to translate to see if we could spot the mention of the equals sign. Recorde also invented new English mathematical words with many not surviving common usage today. Language is something that changes through time and perhaps in a 100 years some of the maths terms we use today will be obsolete too.
I really enjoyed this workshop, it flowed very well, was paced just right and left me with curiosity to go and explore more.
Workshop 4 : No gimmicks learning and teaching using Algebra tiles
This workshop was delivered by Bernie Westacott who I recently found out about after his video podcast with Craig Barton on manipulatives. I very highly recommend watching that video series. Bernie has an incredible depth of knowledge in the use of manipulatives and in particular getting the teaching for young children absolutely correct the first time round. Not only that but introduces algebra right at the start when children first start their maths journey without using the notations yet. I got to meet him the week before for the first time at another workshop in London and this week he had a packed audience ready to get into virtual manipulatives.

The workshop was based around the use of virtual manipulatives app brainingcamp. We spent some time exploring the use of double sided counters and then algebra tiles. Bernie also uses real counters when teaching young children. Incredibly enough he does that without using any symbols or written work, yet he can start getting children to understand the ‘rules of negative numbers’ and even simple simultaneous equations. Young children are perfectly comfortable with the ‘upside down’ world of negative numbers for instance once they have had a play with the counters.

Like Jonathan Hall he also started off with the field axiom of mathematics on the idea of there being an ‘additive inverse’ rather than ‘takeaway’ for the idea of subtraction. He stressed that there is no such thing as ‘takeaway’ at all. The app is a great way to show the additive inverse, the zero pairs can be greyed out when brought close to each other which is pretty neat. These zero pairs can also be used in teaching Chemistry as the positive and negative charges can be used to model electrons, protons etc. I use coloured dots in chemistry teaching as well. But that’s a seperate blog post altogether.
Bernie showed us very elegantly with the counters how a negative of a negative gets back to a positive. What it means to add a negative to a positive and to a negative. And the moment that got the biggest ahhh moment was a demonstration of how multiplying a negative with another negative gives a positive. The clarity and evidence given by this representation using the field axiom idea is irrefutable

There was a little demo of Alge disks then, which seem to be a halfway house between algebra tiles and place value counters. The difference being that instead of numbers the counters have x and y labels on them. Factorising using these disks seemed to tie in very well with the factorising I had seen earlier in Jonathan Hall’s workshop.
We then moved on to algebra tiles themselves. The tiles can be used for a number of things and I have been using them for nearly two years now. Though I only use them for showing the area model and how they can be used to factorise quadratic equations. There’s loads you can do with them, including zero pairs that disappear when merged together
Finally Bernie stressed the point made at the introduction once more that these representations are only there for students to slowly learn and get a feel and sense for what the abstract version of such representations should lead to. And that with time the use of manipulatives need to be faded out of use. They can of course always be bought back as and when necessary on a topic per topic basis in the non linear journey of learning maths as and when required. Which is exactly what I do as a tutor. Bernie now also has a video channel that I recommend watching.
Workshop 5 : Yes But Constructions
The final workshop of the event was delivered by Ed Southall, author of the books ‘Yes, but why?’ and ‘Geometry snacks’ fame. Constructions as a topic is really interesting to me, having done lots of constructions during my Mechanical Engineering degree. In first year drawings are all done on paper with proper equipment before moving on to CAD after that. And subsequently practical sheet metal requires the use of constructions with good equipment.

Constructions for teaching school students is none of that however, it is mostly wobbly compasses, broken pencil leads and nothing ever quite lining up. And teaching it online is a pain as well with the document camera kinda getting in the way. Mathspad and Bitpaper help me though and are usually enough. But I just get the bare minimum done that way.

Before starting any construction work whatsoever it is important to make sure the very hardware students will use is in reasonable working order, fastening the compass screw tight so it is not wobbly and making sure the pencil is not very sharp. Keeping it a little blunt makes the lines a little thicker and gives scope for covering up a little when things don’t match. Just getting used to joining up two points into a line requires practice and fluency (this always seems to have some degree of randomness as the pencil may not follow the ruler track as we think it does) and getting used to drawing circles of various diameters.
We then moved to perpendicular bisectors, bisecting it the classic way. But making sure to draw the full circles so the symmetry and context behind it all is clear to see. In fact drawing full circles instead of arcs is always recommended. Except for when your line is at the bottom of the page, then what? Enter alternative forms of bisecting a line.

Next up was angle bisection “The Don” method and another one. We also did an exercise with circles and lines, eventually leading to something looking very pleasing to the eye in an islamic art type style.

And I learnt about a special type of triangle called a Reuleaux triangle. I finally know what the shape of my guitar plectrum is called and why it rolls so nicely!
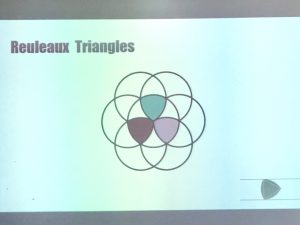
There was also drawing an incircle of a square, incircle of a triangle and a circumcircle of a triangle (see video).
While teaching and leaving a class to do the constructions Ed suggested having gifs of constructions on a loop so students can look at them if they missed a particular step during the presentation so they can go back to it and see the whole sequence. He does this very well indeed on his own twitter account with the gifs which I highly recommend looking at.
Overall another great workshop with loads of great ideas to take away and implement.
A superb experience from the Friday to conference day
The workshops and the entire day is very carefully planned to bring maximum benefit to the delegates and also to make sure as many teachers get to know each other as possible through the various tea breaks, lunch, tweetup event, exhibition, speed dating etc. Penistone was not an easy location to get to particularly for those like me who don’t drive but once you got there it was difficult not to be wowed by the idyllic location and the spacious school layout which made the day feel so much more relaxed despite so much going on.
I say it every time but quite genuinely this was again my most favourite maths conference. I learn so much from everyone, not just the workshops but from every conversation with a maths teacher. With so many new things to try out and full of inspiration I am ready and refreshed for some light summer tutoring followed by a brand new academic year.