Maths Conference Bristol #MathsConf18
This blog post is a write up of my fifth maths conference held on 9th March 2019 in Bristol. Run by La Salle Education, the conferences are attended by around 400 maths teachers, trainers, suppliers, academics, tutors and just about anyone who is passionately into maths education. The maths teaching ecosystem is very diverse indeed and I learn so much from fellow professionals who live and breathe maths teaching. In this post I cover my thoughts straight after the conference with some reflection on how I have used what I learnt nearly 3 months ago.
TLDR ; I got a deeper appreciation of the idea of unity, the unit, one.
Pre-conference Friday drinks
As on previous occasions I travelled up to conference city on the Friday afternoon to tutor my Friday evening students online from the hotel room. After tutoring I headed to the Friday night pre-conference drinks; one of my absolute favourite parts of the whole experience. Conference day on Saturday is an intense day so I really like the Friday to relax into it all over some drinks. At the bar I got a chance to check in and catch up with some of the teachers I’ve got to know through La Salle and I also made some new connections. Tutoring is an isolated profession and it is so useful to share experiences with other maths teachers.
When the bar closed there was only one thing to do, go to another bar. And like Manchester #mathsconf15, the last men standing ended up exploring the nightclub scene. An epic time was had dancing to 1990s tunes.
Onwards to conference day itself.
Workshop 1 : Rekenreks rock, the new manipulative on the block
This workshop was delivered by Amy How who has recently become the ambassador of this invaluable manipulative. I learned about this manipulative recently from the Bernie Westacott video podcast with Craig Barton and from Mark McCourt’s workshops on CPAL and Multiple representations. Since I work with a few Dyscalculia students I am always seeking new ways of developing number sense for students. The Rekenrek turned out to be a tool that can be used for far more than developing number sense alone.

I used the Rekenrek for about two months previous to this conference for number bond work, doubles and subtraction but nothing more than that so far. So frankly I was blown away by how much more is possible with this manipulative from Amy’s workshop. Starting from the very simple idea:
- Build it
- Say it
- Write it
The building part is moving the red and white beads, saying affirms the language and writing it gets it into symbolic form. Amy showed us how to use the beads to show the times tables in action through various arrangements. The patterns that started to emerge by exploring the six times tables got some aha moments in the room.
The 100 bead rekenrek can be used to build fluency for the number bonds of 50, 100, rounding and working out the times tables. We moved to the idea that a 10-row 100 bead rekenrek could also just represent one. Meaning that the same manipulative can also be used to embed the idea of fractions, decimals and proportional thinking. It is so clear and obvious when two fifths of 30 is explored by selecting two rows (of 10 each) out of five. There is an elegance and clarity to using this manipulative and while I initially made the mistake of thinking they are suitable for just number bond work, I have started using these with older students for fractions, decimals, percentages and ratio work.
One other small but important thing I implemented straightaway after this workshop was the idea of “one finger one push” to move the beads. Previously if students were to count the beads out by touching them and moving them one by one then I would let them do that. I realised that for one of my tutees who counts in clusters of one, this had to be corrected immediately. 3 months on and I have used this manipulative with various tutees now, including a superb virtual version of it on the mathsbot site.
Amy’s workshop had primed me with the idea that we can make something ‘one’ and then work from there. This theme of one or the unit then ended up repeating in nearly all the workshops I attended.
Workshop 2 : Cuisenaire rods, Metallica and the one
This workshop was given by Drew Foster who is a big fan of puzzles, manipulatives and hosts #BrewEdPreston. I got a set of original Cuisenaire rods back in 2015 after my Dyscalculia training with Patricia Babtie. For a good three years I used them mostly for number bond and number sense work. I have become more drawn in and fascinated tutoring number bonds over the last 3 years, there is something very profound about them. A few months ago I got some training on how to use Cuisenaire rods from the La Salle CPAL and Multiple representations CPD courses which has accelerated my use of these to no end. I am starting to find so many ways in which you can use these, with students at various stages of their maths learning journey. They are so useful for secondary maths as well; from arithmetic sequences, linear equations, ratios, percentages, area scaling, volume scaling and surface area to volume ratio. I am merely at the tip of the iceberg in terms of their full application.

Drew gave each table a set of Cuisenaires to play around with and move about. He stressed the idea that we should try and see things from the children’s point of view. You have to move these around physically first until stumbling into the right answer through the right combination of the rods. I was making the mistake initially of trying to do things in my heads and then move the rods about. We did a bunch of basic exercises at first from setting up equations in colour, to staircases and a pyramid.
The moments that wowed us all were how a simple ‘up and down staircase’ which looks like a Stats distribution and is linked to square numbers as well. We were also shown how Quadratic factorisation could be shown using the rods. Although I have used Algebra tiles for quadratic factorisation I never linked it using it with cuisenaire rods.

We were shown the video below which is the ‘cuisenaire rods way of the zen’. All to the soundtrack of Enter Sandman by Metallica, my head was bobbing along for that one for sure or was that from the Macarena a few hours earlier at Popworld?
The fact that you can make one anything you like and then the other rods take on a different value is very profound. A couple of tutor colleagues who were at the workshop have now bought their own cuisenaire sets, remembering not to buy any sets with graduations or marks on them which Drew stressed are not the right type of rods. They must have no writing or markings on them. The beauty of these rods is that by keeping them free of any markings you can make them whatever value you want them to take. I was so inspired by this workshop to use this manipulative more and a few months on I have innovated their use in online tutoring ever more. I intend to write more about this in future blog posts.
Workshop 3 : Creativity and Curiosity, there’s more to maths than convergence
Even if creativity is not assessed it is important
As a tutor I often feel the pressure in helping a student prepare for an imminent high stakes exam, particularly for Year 11, 13 or 11+/13+ prep. Every tutoring hour has to count, not just the teaching itself but in supporting the tutee, communicating how the system works to the parents and showing the tutee how to revise by themselves in a structured way. Teaching for a test or exam is very ‘convergent’ in that way. There is a right answer to be got as quickly as possible.

Andrew Sharpe’s presentation reminded us why we really got into maths and how creative it can be. We started off with a number grid puzzle and a coordinate grid exercise. It was ok to fumble about and come to the solution, and in that fumbling process is the joy of discovery. Trial, improvement, iterative processes are all part and parcel of the overall learning process in maths. He encouraged us to make up our own puzzles and for students to do so as well.
An exercise in divergent thinking that I remember was of the ‘Alternative Uses Test’ where 10 alternative uses of a brick should be brainstormed. Highly successful people are creative thinkers and problem solving itself is a creative endeavour. Some students like to think divergently rather than convergently, which is certainly something I have encountered as well. Andrew gave plenty of examples using number maths and geometry for the Alternative uses.
This workshop has inspired me to bring that creativity to more of my students. I do some fairly divergent teaching to those who are homeschooled but there is no reason to have elements of it with other tutees. During preparation for an exam gears have to be switched completely but there’s always some scope for creative and explorative thinking. Most importantly this presentation helps me give myself permission that divergent teaching is all part and parcel of overall teaching and in getting the best out of students. Andrew’s presentation for this workshop with some very useful extra resources are on here.
Workshop 4 : Unit Conversions, metre rules and following the multiplicative arrow
Jo Morgan’s in depth series of presentations are invaluable and I often refer to her presentation notes on the other in depth series, all available on her site here. For this topic on unit conversions Jo started off by mentioning that while unit conversions is not a big topic like solving quadratics or angles, it is a topic that often carries a lot of easy marks and students miss out on these.

She mentioned that units are covered first in Year 3 and then consistently again every year until Year 6. In fact students see mixed units like 1 kg 200 grams very early on in their maths journey and often year 6 students can know their millilitre <–> litre conversions better than Year 11 students. I often teach Year 6/7 students back to back with Year 11 ones and have observed this too. Somewhere in the middle years students don’t see unit conversions as often and lose that fluency in this topic. Jo showed us several examples of GCSE students losing fairly straightforward marks on unit conversions, both in the higher and foundation tier from examiner reports and example scripts (AQA and Edexcel boards). Quite often students were losing marks in just getting the simple decision on whether to multiply or divide the conversion factor.
The presentation then followed the structure of following this strategy in converting units.
- Step 1: Be fluent in multiplying and dividing by powers of 10
- Step 2 : Memorise the conversions
- Step 3 : Perform the conversions
Step 1 is a self evident prerequisite and so Jo covered the other two steps.
Step 2 is all about memorising and recalling the conversion factors. There are surprisingly few conversions to be memorised for GCSE maths in the full range of conversions and all these are given below from one of the slide presentations. I have highlighted in purple the ones that need to be memorised.

This then lead to the discussion and history on why the adoption of the metric system. One interesting fact that I didn’t know was that the prefixes for bigger units (kilo, hecto, deca etc.) are Greek and the smaller ones are Latin (centi, deci, milli etc.). Definitely very useful to know and a great point of discussion for A Level Physics students who need to be aware of the fuller spectrum of units.
To remember units using manipulatives Jo mentioned that an actual metre rule is essential to show to students and water bottles also help. I really like bottles of water in addition to how useful they are to get a feel for volumes. They have lots of lovely Chemistry stuff on the labels, including the ions present, the charge on them, the exact type of plastic (polymerisation) and the concentration of the ions (a compound unit in chemistry that GCSE students also need to know). Lots of Chemistry and maths in water bottles.
Step 3 is carrying out the strategy once students have memorised the actual conversions. There are a number of methods possible, from ratio tables to Don Steward type grids and for calculator papers it can all be done on the new Classwiz calculators. This is very useful to know as I have a few IGCSE students who would benefit from getting the new calculators as both their papers are calculators.
The method that really appealed to me was ratio tables. I have seen them appear on twitter but only during the talk I realised how invaluable a technique it is, a very simple layout with the arrows representing the direction of multiplication. Going against the arrow means to divide. This will be very handy indeed for many of my students. The method that was very popular amongst maths teachers was “Last man standing”. It is a neat method using the idea that (100cm/1m) can be expressed as 1 and then the units can be ‘cancelled down’. I’ll refer to the excellent interpretation of Last Man Standing by Mr. Bracewell and Jo’s presentation slides referenced earlier.
This presentation gave me plenty of thought on another interpretation of the unit as being one and how you can use it convert between units. I tutor the Sciences at GCSE as well and dimensional analysis is very useful indeed there. Ratio tables to convert between units is something I certainly want to implement and last man standing is a useful new technique to have in the teaching toolbox.
Nearly three months on the thing I have used most is the use of ratio tables with my two GCSE retake tutees, particularly the idea of ‘going against the arrow’ to divide. Teaching students for an imminent exam when time is short does require such shortcuts which I feel can be justified for the long term benefits it will bring to the student’s future chances. As for what division sense actually is and how to convey the idea to students over the long term, that was covered in the next workshop.
Workshop 5 : Time to revisit…Division, the beast of division tackled
This was the first time I attended one of Pete Mattock’s talks having chatted to him before about the use of Algebra tiles and other manipulatives. In the preview blog post for this workshop he mentioned that “Professor Emeritus in the department of education at the University of Oxford calls division ‘The Dragon’. Those pupils who slay ‘The Dragon’ tend to go on to do well in mathematics; whilst those who don’t tend to struggle from that point on.”

There’s certainly a lot of truth in this. Making sense of division has many important implications further down the line, including unit conversions which I had just seen on the workshop before. By being able to make sense of the division process from the very outset using the appropriate concrete and pictorial methods as support, a long term framework can be built up for pupils to understand the process of division. Concrete and pictorial methods eventually being faded out. I am currently reading Pete’s book ‘Visible Maths’ that looks at a variety of topics from different representations of whole numbers, powers and roots, the laws of arithmetic to algebraic manipulations. Division being just one of the topics in that book that was presented during this workshop.
Double sided counters and cuisenaire rods were the two manipulatives used during this workshop with delegates having ample opportunity to move the manipulatives around on each table. Counters being used to show the discrete view of division. 12 ÷ 3 can be shown as 12 being put into groups with 3 counters in each group (creating 4 groups) or 12 being shared into 3 shares (with 4 counters in each share).
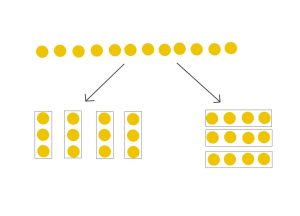
Using the other side of the counters can then be used to show division where negative integers are involved. The red side of the counter represents -1 while the yellow side represents +1. Putting a red and yellow counter together creates a zero pair. Having a line of 12 reds represents -12 which are then put into groups containing three -1 counters, representing -3 together. Thus creating 4 groups.
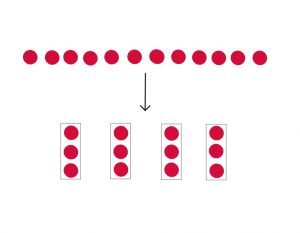
300 ÷ 20 can be demonstrated by making the 20 as 1 (in the same way as shown in Drew’s earlier workshop). Once the cuisenaire train of 20 is 1 then it is easy to make a multiplicative comparison with 300. 15 multiples of the ‘1’ unit.
And how to tackle the beast of division itself? Division and fractions. Again a multiplicative comparison is used to compare part to “whole”. The part being assigned the value of 1. Pete talks about fraction division in his podcast with Mr Barton, which is an excellent and more comprehensive description of the idea.
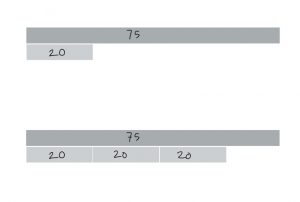
We finished off with a practical context where a simple speed, distance, time context could be visualised using the idea of multiplicative comparison. Speed is the distance travelled in unit time, i.e the distance traveled in one hour, one minute, one second etc. The example used was finding the time when 75 miles are covered at an average speed of 20 miles per hour. Once again 20 is made into the unit, i.e one. There are 3 of those complete units of 1 hour time ‘blocks’ and a remainder. The remainder being 15 out of 20 = ¾.
The idea that really stuck with me, from Pete, Jo, Amy and Drew’s workshops being that the ‘unit’ is of profound significance. Exactly what that means was summed up by a tutee of mine in the last days of GCSE exam preparation with the quote at the end of this blog post.
Summing up the whole experience, this was by far my most favourite MathsConf so far. I am grateful to all those teachers who put in so much effort to run these workshops for the rest of us. And big thanks to the La Salle team and visionary Mark McCourt for putting these together.
Nearly 3 months after this conference and just days before the final IGCSE paper, my retake tutee exclaimed with delight in that light bulb ‘aha’ moment that we teachers all live to experience.
Once you know one, you know everything!
Mission accomplished, so many things fell into place for my tutee in that moment of realisation. I can’t wait for #MathsConf19.
I am so excited to be reviewed in such a professional manner. Your comments are incredibly positive and help me to continue to be the “ambassador” for the rekenrek… Which is my dream. Thank you so much. I am humbled.
It was my pleasure to write about your workshop. I could have spent ages not knowing to get students to use the ‘one finger, one push’ idea so I am glad I learnt the correct way to use the manipulative and got so many new ideas on how to use this. Several of my tutees now have their own rekenreks as a result in my increased confidence of using it. I have just bought your book as well which will be very useful.