MathsConf39 London: Back to Where It All Began 8 Years Ago
Complete Mathematics do something truly phenomenal for education. They bring mathematics teachers who live and breathe teaching under one roof. Thanks to this network, my teaching has been utterly transformed in the last 8 years.
In 2017, I nervously went to my first ever maths conference, #MathsConf10 knowing no one. I have now attended 20 in-person and 6 online conferences since, traveling all round the country. But this time I didn’t need to spend hours on trains and book any hotel rooms.

A big part of the experience is the Friday night pub social before the conference Saturday. This one was lively yet relaxed as I caught up with old friends and made new ones. I’ve had a tough year as mentioned at the last conference write up. So being in the company of other maths teaching lovers was just what the doctor ordered.
These chats are perhaps at the entire heart of the maths conference experience. I go back to what Mark McCourt used to say at every conference intro :
“Imagine how good it would be if all mathematics teachers in the country became friends with each other.”

On to conference day itself, there was a real buzz in the air as 350 delegates arrived and it was so good to see attendance climb back up to pre-pandemic levels. There were 35 workshops and we could only choose 5, so I chose as well as I possibly could.
Workshop 1 : Teaching Backwards To Secure Success by Jack Jennings
Being a fan of backwards fading I signed up to this one immediately. However, Jack made clear at the start that this was not a backwards fading workshop or about solving challenging questions. This was more like Atomisation 2.0 (in his own words). Three things from this workshop resonated with me the most:
Hard to learn, easy to forget
Students remember the start of a process much better than the end. As working memory gets used up, the final steps are where attention fades and mistakes creep in. Teaching backwards tackles exactly this. One of the paragraphs from Jack’s slides summed this up perfectly:
Temporal Effects: Research indicates that students often remember the beginning of a process better than the end. This phenomenon, known as the “serial position effect,” suggests that initial steps are more easily recalled due to their recency in the task execution or their distinctiveness.

Adding only (initially) instead of subtracting in Simultaneous Equations
When teaching simultaneous equations, Jack doesn’t bother with the whole “Same Sign Subtract” thing anymore. Instead, his students always add. If the question would normally need subtraction, they just multiply one equation by –1 and add instead. Naturally, by that stage his students would be fluent in shaping and changing equalities.
I loved this! Clean, and one big decision taken out completely. It lowers cognitive load and nips potential errors further downstream. I am going to steal this one and experiment with it.

Crack the hardest topic and open the confidence floodgates
By getting his Foundation students to master one of the toughest topics early on and telling them something like:
“If you can do one of the hardest topics on the course, then the rest will all fall into place”
Once students get that win under their belt, their confidence floodgates open. The psychological effect compounds improving motivation and emotional resilience. It seems like a huge time investment to teach this topic in a highly atomised way, especially when there is a curriculum to get through. But this time investment compounds learning gains so much later. Playing the long game is where it is at.

Workshop 2 : The Best That Has Been Taught and Shared (aka What makes a great task?) by Nathan Day
I have the utmost respect for those who design brilliant tasks, as it is no easy task (intended pun just for Nathan!). Nathan is known for his website interwovenmaths.com which is full of rich tasks that link various areas of mathematics together. He presented about this at #MathsConf28

This workshop was a tour of some superb tasks and reflections on why they worked so well. He arranged us into groups of 3 or 4 and flipped the narrative back for rich group discussions. We got to discuss the four prompts shown on his starter slide here for various tasks. Nathan mentioned how that by attending many conferences over the years he learnt so much just from conversations with colleagues on CPD. And that he wanted to ensure that his workshop is more a collaboration of teachers talking to each other, rather than him present information one-way for a whole 50 minutes.

Conversations there were plenty of. Every one of the tasks he showed were new to me. It was a joy to think mathematically and to think how I could adapt these tasks with my own tutees. Here are some photos of the 17 tasks that were shared. The tasks are beautiful and can do the talking themselves here.

Workshop 3 : Reintroducing Don Steward by Jo Morgan
“The utter genius and joy of using Don Steward tasks by @mathsjem”
I tweeted this and attached photos of three Don Steward tasks that Jo discussed. To my surprise I saw twitter spring back to life for a second, a life that I haven’t seen there in years. Comments, retweets and even eager task solvers were on to this. What a testament to the late Don Steward that his tasks still spark this kind of collective mathematical curiosity.

Jo’s workshops are always jam-packed with value, and this one was no exception. I am a little embarrassed to admit that I’ve barely scratched the surface of his work myself. Apart from using the fantastic averages tasks on MathsBot, I hadn’t really explored the rest. Jo pointed out that with the decline of “Maths CPD Twitter/X,” many newer teachers have simply never heard of Don Steward. There are other reasons too. In my case, I’d always assumed his tasks were mainly for stretch or high-attaining students. But after seeing the sheer range Jo showcased, I realised how wrong I was. I’ve got a real treat ahead exploring and using more of these in my teaching.

Another reason Jo mentioned for the lack of take up of his resources is that Don never provided answers to his tasks. He didn’t want students to simply look the answers up up online, and more importantly, he wanted teachers to do the tasks themselves first. That excuse doesn’t hold anymore. As Jo pointed out, AI (for all its flaws) is very useful here as it will work out all the answers, though it does get the odd one wrong. Don would have approved no doubt as it will keep teachers on their toes!

On the surface, his tasks look simple and accessible, but underneath lie layers of depth and the opportunity for purposeful practice. They are easy to get into, have superb variation and as pupils engage with them, patterns emerge (like all the questions having the same answer). Don had a rare gift for designing tasks that draw students into noticing structure and asking “why?” while keeping them curious.
He was a pro at visual design too and his minimalist layout reduced visual cognitive load. He often included one or two answers that broke a pattern to keep students (and teachers) awake. Some of the answers had a pattern that helped busy teachers teach between tables and check all answers quickly. Even the little cartoons he sprinkled in were witty without being distracting. The mark of someone who understood teaching at all levels and facets deeply.

His Median blog is a goldmine in maths education: hundreds of carefully curated, classroom-tested tasks covering the entire curriculum, shared freely and generously. He refined his work in real classrooms over decades, and it shows.
Sadly, Don passed away from Covid in 2020. Jo spoke fondly of meeting him and collaborating to popularise his resources online. Her session was both a masterclass in task design and a heartfelt tribute to someone whose work has genuinely changed the landscape of maths teaching.

Workshop 4 : What is number sense and how do I teach it? by Jo Austen
Teaching early mathematics to young learners and Dyscalculics is an obsession of mine. It stretches me as a tutor enormously, and over the past decade it’s where I’ve experienced the most growth. And humility too, as I know I have a lot further to go still. In my experience, teaching early/primary mathematics thoroughly in a forward facing way is far more demanding than teaching secondary mathematics. You are building the entire structure of mathematical understanding from the ground up. Number sense, place value, part–whole relationships and language/vocabulary/comprehension. Getting this right requires a level of linguistic pedagogical precision, responsiveness and representational fluency that’s both daunting and exhilarating.
Jo started his session by passing around a box of fudge sweets while we tried to guess how many were in there. One person got it spot on at 44 and won the sweets. A great estimation exercise.
Some ideas that stuck with me from the workshop were:
Cardinality – Making a ‘number museum’
The idea of fiveness is surprisingly complex and abstract, I mirror it with the idea of ‘redness’ or ‘catness’ when teaching this to tutees. But to actually go out and make a number museum is such a brilliant, hands-on way to explore cardinality. I’m definitely going to start using it straight away, with my 6-year-old nephew and 2-year-old niece as perfect guinea pigs.

Distractions from Cardinality
Teaching number sense is very hard, the meaning of ‘more’ can be interpreted in so many ways. In each example you can see why a child might declare there are more pink cubes than blue cubes.


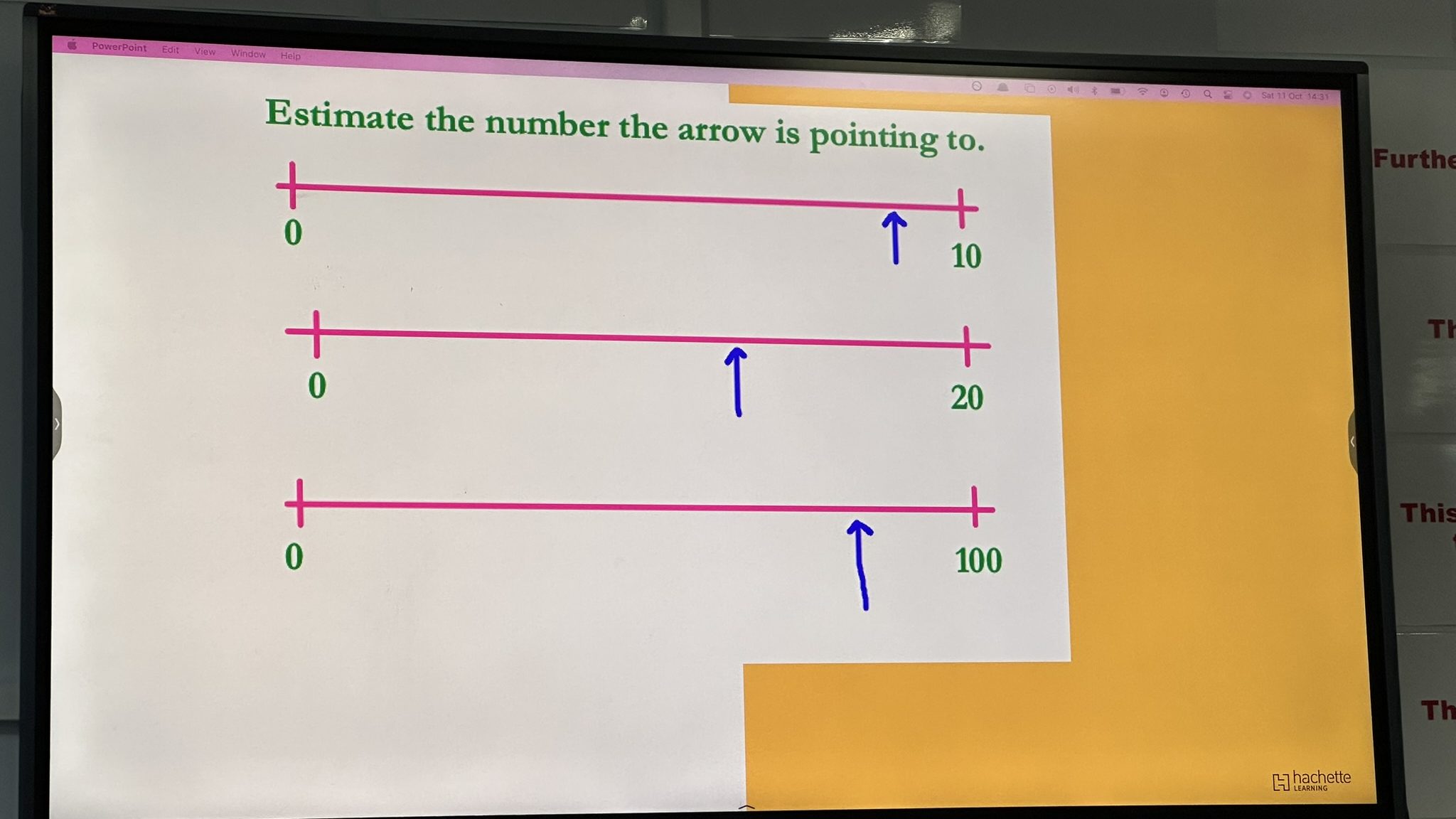
Departing from discrete number representations and into number lines
Moving from counting actual things to understanding numbers as positions in space, where quantity lives in the distance from zero is a massive conceptual leap. Jo’s examples in getting pupils to place 6 on lines with different scales, or estimate where an arrow’s pointing seem easy to us, but they’re anything but. These tasks need solid part–whole understanding, proportional thinking, and good spatial mapping. Jo shared several number line resources with us. These included double labelled number lines and excellent zoomable number lines on mathsisfun.

Additive reasoning or multiplicative? The £10 twins
Jo also threw in this brilliant prompt along the lines of:
“What’s more fair? Mum gives one twin £10 and the other £20. Years later she gives them £9990 and £10,000.”
The question pushes students to move beyond simple additive thinking (“how much more?”) and start reasoning proportionally. In the first scenario, one twin gets double what the other does; in the second, the difference is tiny. But how big do the numbers have to be before doubling becomes proportionally more than just adding? What a brilliant prompt that has a lot of mileage.
1, 2, 3, 4, 10, 100 and….a million

Young children are fascinated with big numbers. And it is so hard to get a sense of really big numbers like a million. Jo mentioned the “How Big Is a Million?” book that I had never heard of before. Through the story of a little penguin searching for something as big as a million and eventually finding a sky full of stars, Jo gave students a tangible, emotional anchor for what that number means.
Other things I remember from the workshop were the use of decimal squares and Gattegno charts, both on the mathsbot site.
Overall, another great workshop by Jo leaving me with plenty to think about and some actionable resources straight away. Jo has a book out called ‘Small Numbers, Big Ideas: Essential Concepts for Teaching Early Maths’. I have ordered it and can’t wait to learn from more.
Workshop 5 : History of Mathematics themes in Maths Lessons: Why and How? by Thomas Briggs & Jason Yip
The final workshop of the day was a tough choice with so many others to choose from but being a total mathematics history nut, I had to go for this one. In fact, using history in teaching mathematics was my last blog post.
Jason kicked things off by going through a study on how introducing mathematics history was perceived by pupils at schools. While Tom opened his part of the session with:
“I know music teachers who’re in choirs; English teachers who read (voraciously) at home; PE teachers in football teams; & history teachers who often visit museums. But most maths teachers I know don’t go anywhere near the subject when they’re not working.”

Now, most people in the active maths CPD network do go near the subject when not working (otherwise we’d not be there at the mathsconf, or blogging about it or reading about it!). But we all know colleagues who only do or talk maths when teaching. Even getting colleagues to come to a maths conference is a struggle.
For the rest of us maths enthusiasts, Tom recommended checking out your local MathsJam which are informal monthly meetups for anyone who enjoys playing with maths.
Two specific history bits that stuck out to me were about the Rhind Papyrus and the invention of the equals symbol.
Robert Recorde and = (as well as +)
Gareth Jones focused just on the history of Robert Recorde at his excellent workshop at #MathsConf28 that I reviewed, as well as the YouTube #MathsChatLive later.
Jo Morgan also covered Robert Recorde in her mathematical vocabulary workshop at #MathsConf19.
The Rhind Mathematical Papyrus
Discovered in Luxor (Egypt) and bought in 1858 by Scottish antiquarian Alexander Henry Rhind, it now lives in the British Museum. Also known as the Ahmes Papyrus, is basically one of the earliest maths exercise books we’ve got. Dating back to around 1550 BCE, it’s crammed with 84 problems on arithmetic, geometry, fractions, proportions, and loads of practical calculations. Including a surprising obsession with sharing loaves of bread, which Tom found pretty funny. It was copied by the scribe Ahmes from an even older source, giving us a glimpse into Egyptian maths more than a thousand years before the Greeks.
What’s amazing is how familiar it feels: clear worked examples, step-by-step methods, and down-to-earth problems. It is like opening a time capsule and finding a beautifully structured maths workbook where maths questions were made up using loaves nonetheless.

Other history of mathematics resources for teaching
- Timeline of Mathematics – Fantastic interactive by mathigon
- A History of Mathematics Paperback by Carl B. Boyer (Author), Uta C. Merzbach (Author), Isaac Asimov (Foreword) – A very complete and comprehensive book
- Introducing Mathematics: A Graphic Guide (Graphic Guides) Paperback by Jerry Ravetz (Author), Ziauddin Sardar (Author), Borin Van Loon (Illustrator) – A sort of comic, surprisingly comprehensive for a small book
- The Story of Maths – BBC Documentary by Marcus Du Sutoy
- Nathan Day – The History and Future of Mathematics
And of course, there is Tom’s new book ‘The Mathematician’s Library, by Thomas K. Briggs’ which I bought already before the workshop. It is beautifully illustrated and curated.
Finally, Tom and Jason also announced their new project: The History and Maths in Education Network. It’s designed to bring together teachers interested in using historical themes to enrich maths education, sharing resources, ideas, and conversations. I have joined already.
Final thoughts – A buzzing day, the march of AI, and a fragmented online maths community
Outside the workshops, the usual MathsConf buzz was kept alive by various stands from education companies, Rob’s unmistakable tuck shop, a maths mingle, treasure hunt, raffle… the whole works.
There weren’t many sessions explicitly on manipulatives this time, perhaps just coincidence or they’re out of fashion a little. There were plenty of manipulatives mentioned in some of the workshops I attended though.
AI cropped up several times. Jack used it to create atomised drills, Jo used it to check Don Steward answers, and I use it for drills, maths history rabbit holes and well, even editing this blog post. For better or for worse, AI is weaving its way into maths education and we will no doubt see workshops on it in the future.
One thing I can’t ignore is how much I miss the old maths Twitter. It was at the heart of so much maths CPD : blogs, podcasts, tasks being shared, conference reflections, late-night debates and so much more. Now it’s a fragmented mess spread across X, Mastodon, Bluesky, Facebook, LinkedIn, and goodness knows where else. It’s such a loss. I do hope a strong online community space eventually pulls us all back together again.
It was also brilliant finally meeting Priya Shah, Anne, and Darren Elgar in person together, we are regulars of the Prof Mahesh Sharma CPD network.

Nearly two days since the conference ended, I am still absolutely buzzing from what I learnt and all the conversations I had. Thanks to the everyone who presented and the entire complete mathematics team for making the magic happen behind the scenes. Long may it continue!



One Comment