Category Archives: Uncategorized

Unary and Binary Operations: The Hidden Architecture Beneath Every Maths Calculation

Leave a Reply

BIDMAS is a lie. And your child deserves better.
It’s not real maths — just a shortcut masquerading as understanding.
Most children are taught to follow it blindly, without ever learning what an operation truly is.
Unary. Binary. This is the hidden architecture of calculation — in primary, secondary, and beyond.
And it changes everything once seen.

But first, an actual story from tutoring.

“Why do I keep getting this wrong?”
My student looked at me with a mix of frustration and helplessness.

We were trying to rearrange the cosine rule to isolate the angle. But he kept adding a², b² and the -2bc terms together first. Again. And again. Each attempt revealed something deeper: he wasn’t just making a slip, he was missing something fundamental about how mathematical operations are structured.

Watch: Unary vs Binary Operations Explained Visually Using Function Machines – a concept every student should understand but rarely gets taught.

After three years of working together, I felt like a failure, I had missed my chance to embed into him essential structural ideas. The fundamental ideas of operations and the Field Axioms. I almost certainly taught this to him but it was a long time back and he needed regular recaps. With the exam just a week away, I did what many tutors do under pressure, I gave him the rearranged formula and told him to memorise it.

This wasn’t a struggling student by any means. He was on track to get at least a grade 8 (for the GCSE qualification in the UK at KS4). And yet, after 11 years of schooling, this foundational misunderstanding had gone unaddressed. The system he learnt from was rewarding performance, not depth. Not structure. Not true mathematical thinking. Only the odd questions like this would unearth this weakness.

So what had been overlooked for this tutee?

One of the most overlooked—and surprisingly simple—concepts in school mathematics is understanding what unary and binary operations are, and how they differ. I was first introduced to binary operations through Professor Mahesh Sharma’s engaging and interactive CPD webinars.

It lies at the root of every mathematics calculation your child will ever do. And almost no one teaches it.

What Do Unary and Binary Mean?

Let’s start with some etymlogy.

  • Unary comes from the Latin unus, meaning one — think : unified, union, uno (Spanish)
  • Binary comes from bi, meaning two — as in bicycle, bipedal, or bilingual.

In mathematics, these root meanings give us a simple but powerful distinction:

  • A unary operation acts on one input.
  • A binary operation acts on two inputs.
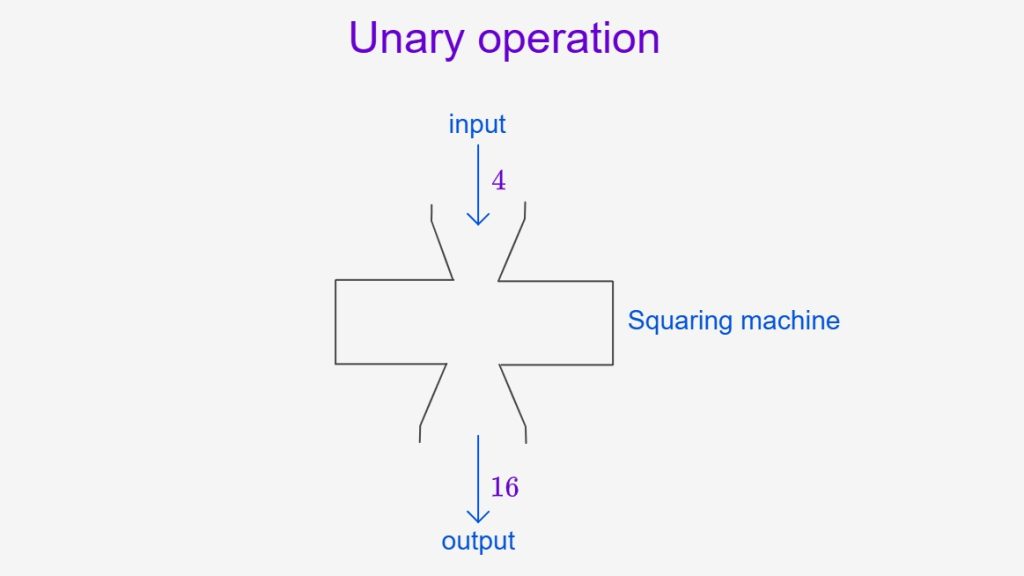
Unary operation: A single input is transformed by one operation : a structure students use without realising it.

Unary Operations – One Input

When the input is a single number, unary operations take that single number and transform it.

Unary operations, involve just one number: squaring, taking a square root, finding a reciprocal, etc.

Think of it like a machine:

1 number goes in → 1 number comes out

Examples of Unary Operations:

  • One more than: +1 (as experienced in early mathematics)
  • Negation: changing +5 to –5
  • Absolute value: |–7| = 7
  • Square root: √25 = 5
  • Squaring: 4² = 16
  • Reciprocal: 3⁄8 → 8⁄3
  • Trigonometric functions:
    • sin(30°) = 0.5
    • cos(60°), tan(45°) etc., all take one input (an angle)

In this sense, Unary operations are transformative, not combinational.

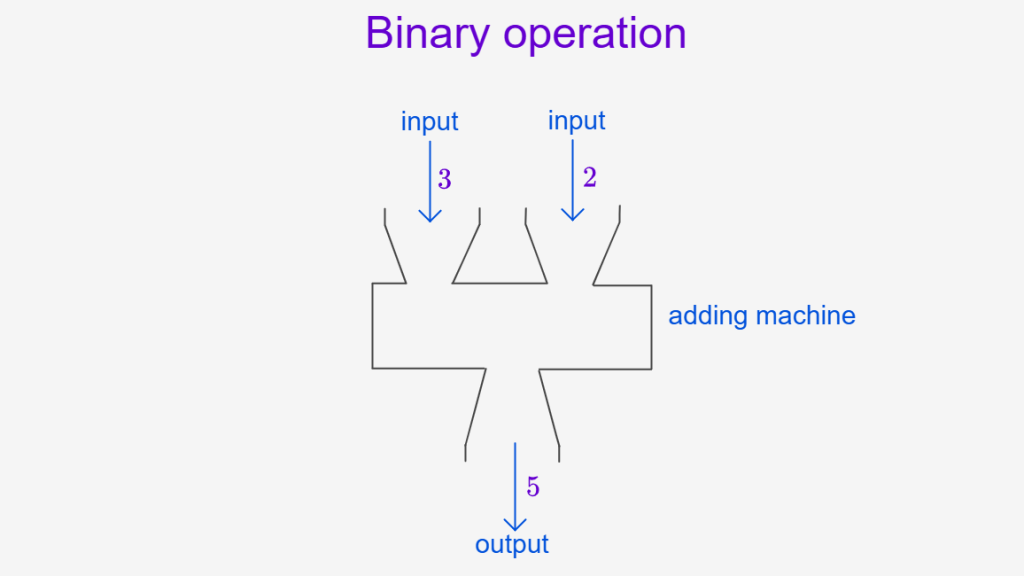
Binary operation: Two inputs combine through a single operation : the backbone of addition, multiplication, and much of school mathematics.

Binary Operations – Two Inputs

Most operations in primary and secondary maths involve two numbers. These are called binary operations — addition, subtraction, multiplication, division, exponentiation etc.

When the inputs are two numbers, binary operations combine values.

Think of it like this:

2 numbers go in → 1 number comes out

Examples of Binary Operations:

  • Addition: 3 + 5 = 8
  • Subtraction: 9 – 2 = 7
  • Multiplication: 4 × 6 = 24
  • Division: 12 ÷ 3 = 4
  • Exponentiation (technically binary): 2³ = 8

Binary operations are the heart of arithmetic. But when students don’t grasp that they are operations on pairs, things get messy fast. Or worse, they are given shortcuts or mnemonics to remember.

Ambiguous cases of Binary Operations

Some operations can appear unary or binary depending on how they’re framed. For example, a “double machine” (×2) or an “add-two/two-more-than” machine” (+2) looks unary but both are really binary operations with one input held constant. Similarly, exponentiation is unary if the exponent is fixed (like squaring or cubing), but binary when both base and exponent vary. This subtlety is part of what makes the structure of maths so powerful and why understanding it matters.

Nullary and Ternary Operations

There are also nullary operations — like random number generators, which require no input — and ternary operations involving three inputs, such as programming conditionals. But unary and binary dominate school maths.

Chaining Binary Operations Vs BIDMAS/PEMDAS etc.

BIDMAS (or PEMDAS in the US) and all of its dreadful mnemonic variants mask the true structure of mathematics. It encourages mechanical order-following, not deep understanding.. But few realise that what they’re doing is chaining binary operations, in a way that only works because of the underlying laws of arithmetic. The underlying laws of arithmetic are the Field Axioms. I first learnt about the axioms from Mark McCourt on a Complete Mathematics CPD day.

The Field Axioms are worthy of an entire series of blog posts which will come up in future. For now, here is a link to a presentation I did at #MathsConf26.

Beyond Numbers: How Unary and Binary Operations Apply to All of Mathematics

Unary and binary operations are the starting point for making sense of all maths operations, from number work to algebra to calculus.

Unary and binary operations aren’t limited to numbers of course, even within school level mathematics. They also apply to vectors, matrices, functions and sets. Except for matrices which are in Further Mathematics A-Level (KS 5), the rest are within the compulsory school maths curriculum.

A more formal and rigorous definition of unary and binary operations is covered in mathematics degrees, considering the idea of sets and closure. But the essential idea of it is very simple and there is no reason whatsoever to not to introduce that idea at school level mathematics.

I will cover the definition of operations, operators and operands on another dedicated blog post.

Final Thoughts

Unary and binary operations aren’t just abstract definitions, along with the Field Axioms they’re the hidden structure behind every mathematics problem your child will ever face at school. Like the grammar and syntax of language.

Without this grounding, students:

  • Memorise blindly
  • Struggle with multi-step algebra and arithmetic
  • Misapply order of operations

With it, they begin to:

  • Understand structure
  • Build and deconstruct expressions logically
  • Think mathematically
  • Have inner confidence that mathematics makes perfect sense

Try creating your own ‘operation machines’ and have a play at putting inputs and seeing outputs. It may be obvious but you’d be surprised by what it reveals when you put it in this format.

What do you think?

This was a fun and educational blog to research and publish. Some references and tools I used to clarify my own understanding further were WikiPedia, mathsisfun.com, Study.com and ChatGPT.

Education and communication are on-going dialogue. I would love to hear your reflections on this. Especially if you are a teacher/tutor colleague.

If you’re a parent who wants your child to learn maths like this — with clarity, depth, and real understanding — feel free to get in touch.
I occasionally have tutoring slots open for children aged 12 (Year 8 KS3) or younger.
If you’re interested, contact me here to check availability.

Finding Light in the Dark: How MathsConf38 helped me begin again

Leave a Reply

2025 has been the toughest year of my life. I lost both my mother and my aunt (mother’s younger sister).

So returning to MathsConf38 was the ultimate healing I could have asked for.

Complete Mathematics #MathsConf38 pre-conference social.

Teaching mathematics is one of the most amazing things in the world, and doing it for a living reminds me of what a rare and precious gift I have in my life.

I love the subject deeply. And I love how it holds the immense power to transform people in unimaginable, infinite ways. As cliché as it sounds, it is the language of the universe.

But it’s easy to forget that when life gets heavy. Deep in grief, the days blurred into one. Just turning up to teach felt like a challenge. It felt like a lonely world that no one understands.

There were moments I barely held it together. I was thrown around the globe : Buenos Aires, Tokyo, New Delhi, and Londonin less than 2 months. My tango learning from the elite instructor in the world disrupted as I flew back to London to say goodbye to mum. Traveling mid-academic year to unite my mother’s ashses to the holy Ganges in Rishikesh, India. And to reconnect with long lost family.

I had to take time off but I could never leave my Year 11s and Year 13s stranded. I worked with one of my Year 13 tutees for 8 years (we started in Year 5). I had to take him and all my other exam tutees to the end of the line.

In those days, I needed mathematics in my life more than they could ever have known.

And then, like clockwork, the Complete Mathematics conference arrived, gathering the most passionate, curious, and learning-hungry maths teachers under one roof.

I saw this beautiful subject expanded in all its glory through other teachers.
A new viewpoint. A new perspective.

I left feeling grounded again, not just as a teacher, but as a human being who has walked through fire and is slowly, steadily, finding their way back.

Thank you to everyone who made MathsConf38 what it was.
To the brilliant teachers who keep showing up, sharing, learning, and inspiring.
To the kind teacher who gave me an antihistamine as my face puffed up from an allergic reaction due to heat, pollen, travel.
To all that pub chat at the pre-conference social.
To the coffee table buzz during breaks as everyone shared what excited them.
To the wonderful workshop leaders who made me excited to be a student of mathematics again.
To Mark McCourt for starting this show all that time back.
And above all, to the Complete Mathematics team for putting it together.

You helped me more than you’ll ever know.

Mathematicians and poets play with patterns: with words, with symbols, with life. Dan Rose showing exactly that at his workshop.

(I felt inspired and sparred with AI, making my voice more like mine to put this post together)

How I went from failing maths to becoming a global maths tutor

Leave a Reply

By the time I was 11, I had already lived in five different countries. By 13, I had quietly fallen behind in mathematics and failed my end-of-year exam.

Atul Rana
A young school going Atul Rana

It wasn’t for lack of intelligence. It wasn’t even for lack of effort. I was just lost in a cycle of constant school transitions, new languages, and new syllabi. One day I was learning maths in Kenya, and a few months later, I was expected to pick up where another system had left off in India.

By then, I had attended schools in Yemen, Libya, Kenya, India, and the UK. Each change pulled the rug from under my feet a little more. And in maths, a subject that builds on itself, well the cracks had begun to show.

Failing Mathematics and What My Father Did Next

My father, a former mathematics tutor turned Junior Indian diplomat, was stunned when he saw my report card. He had tutored in India for several years and did not believe his eldest child had failed. Quietly. Completely. It wasn’t just a bad grade, it was a warning sign. Something had gone missing in my foundation. In part he felt guilty and responsible for this drift.

And so began one of the most formative summer months of my life.

While my siblings slept through summer, I was up at dawn. My dad tutored me one-on-one, every morning, relentlessly but patiently. We didn’t “catch up” on mathematics, we rebuilt it from the ground up. We didn’t race ahead, we stopped, slowed down, and retrained my mathematical brain. In fact, some pedagogy I learnt from his teaching, I still use today in my own tutoring.

By the end of the summer, I retook the exam and passed with flying colours. But more importantly, I never struggled with mathematics again. The foundation had been laid. The confidence was real. The love of mathematics had now been instilled at a deep level.

From Nomadic Childhood to Global Online Tutor

Looking back now, I realise that experience shaped everything I do today. I grew up across cultures, systems, and continents. I know what it’s like to feel behind. I know the anxiety that builds in students when the gaps keep widening.

Today, as a specialist online tutor, I work with children around the world, some of them relocating like I once did, some of them homeschooled, and many of them quietly struggling with maths anxiety or Dyscalculia.

And for all of them, I offer not just maths tuition but stability, presence, and a long-term approach that heals the damage school transitions often cause.

I become the one consistent figure in their mathematics journey, wherever they are. I am online and I can move to wherever they move to.

Why This Matters

Too often, children who “fail” mathematics early simply give up. The label sticks. The confidence disappears. But most of the time, it is not the child’s fault, it is the system. Or the pace. Or the fact that no one ever went back to rebuild what was missing.

I was lucky. I had my dad. Most children don’t.

Though my father is no longer alive, one of the most important gifts he could have ever given me was the love of mathematics and an ethic to work relentlessly. Thank you dad.

How to teach method selection by articulating internal monologue to pupils

Leave a Reply

We’ve all encountered pupils who stare at test questions blankly despite having a gut feeling on what to do.

When pupils encounter a novel question on an exam, the very first emotions and thoughts they have might be something like this internal monologue:

What is this question?
Where do I begin?
How do I decode what this question is actually asking?
What topic/s could it be about?  
Is it on something we are learning now or something covered some weeks/months/years ago?

Pupils acquire a personal methods toolbox after years of learning mathematics. And they need to learn which method to apply for what question. While this may seem straightforward to us, the value of explicitly articulating this process became apparent after listening to Mark McCourt on a podcast with Craig Barton (1:24:45 onwards).

We can guide our pupils by vocalising an acted out internal monologue, showcasing how an expert would approach the problem. Speaking aloud:

Hmm, OK so I see a right angled triangle.
Pythagoras’ Theorem related?
Trigonometry? 
Or something else?
Two side lengths given, so it could be Pythagoras?
Hang on, let me read the question again to confirm what it is actually asking for, usually the last sentence in the question.
Ah, it asks for an angle.
So, not a Pythagoras’ Theorem question then as that involves side lengths.
Most likely Trigonometry?
Let’s assume so and start this as a Trigonometry question.
I should label all the sides accordingly.
<Labels sides with s,o,h>
Two side lengths given (o and h) and you need to find the angle.
It is a Trigonometry question after all.
The side lengths are given so the inverse sine function will be involved…etc.”

Example from an online maths asynchronous tutoring session for a home-schooled tutee.

But what if no immediate strategy is apparent at all? Welcome to being a real mathematician! It happens to me with tutees sometimes when they drop a question. I role model how to start attacking a question by scribbling out something. Quite often that is re-writing some bits of the problem by sifting through information. Probing the question more with some guessed strategies, poking it with a stick (as Paul Lockhart would say). Some of these strategies will be abandoned later but that is ok because each attempt reveals something new about the problem. All of this is articulated live.

Pretending to be a novice when you are not one is initially challenging but it gets easier the more you do it.

Method selection is part of the “Practice” phase of the Teach-Do-Behave-Practice mastery cycle. It is crucial to differentiate it from the “Teach-Do” phase, which serves different objectives (building automaticity and fluency). Questions at that phase already have cue and recency. If I have just covered 5 questions on finding angles using the inverse sine function then of course the next question will be on that. There is no element of uncertainty in decoding the question from a mixed assortment of topic questions.

Platforms like Corbettmaths 5-a-day provide invaluable practice for pupils to continuously refine their method selection skills. And this practice leads to much better long term understanding.

Over the past five years, I’ve integrated this approach into my tutoring with great success. In forthcoming blog posts, I’ll share case studies in real-world cases.

Ultimately humans learn a lot through observation and mimicry, absorbing not just technical details but also the emotional nuances of problem-solving. By articulating our problem-solving processes and giving pupils a glimpse into ‘under the hood’ thinking, we help pupils hone their own method selection skills. Something they then have forever in their lives.

Maths Conference Gloucester #MathsConf28

Leave a Reply

La Salle Education are the UK’s largest mathematics teacher professional development providers. Their conferences are attended by around 400 maths teachers, trainers, suppliers, academics, tutors and anyone who lives and breathes maths teaching.

#MathsConf28 was an absolute buzz : from Don’t stop interweavin’, going against and along the grain of grids, BIDMAS blues, Robert Recorde’s era of the rock symbol \m/ and jammin’ on jamboard.

Friday night social group shot #MathsConf28
Friday night social group shot. Photo by La Salle Education.

Pre-conference Friday drinks

The Friday night social felt like a pre-pandemic social we knew and loved, a good turnout. I met many teachers and tutors for the first time, some that I got to know very well online and some I just met at the pub. The online conferences and networking over the last two years had drawn a lot of new teachers in.

The drinks and chat flowed until past midnight and for a rare first time, #TeamMathsconfParty took an early night instead of going on to a nightclub.

On to the Saturday.

Conference introduction – first #mathsconf for most and hands on the head game

Mark McCourt (CEO of La Salle), Andrew Taylor (Head of AQA maths – main conference sponsors) and Rhiannon Rainbow (on behalf of Gloucester Academy) opened the day. Mark showcasing the achievements of La Salle in not only providing incredible CPD for maths teachers but the TUTOR platform that is directly helping pupils.

A quick show of hands revealed that most (> two-thirds) delegates were attending their first ever in-person mathsconf.

Rob Smith and Jonathan Hall entertained the masses with a “more than or less than game” where Rob quoted a fact with numbers “E.g In 2018 was Ed Sheeran worth more or less than Daniel Radcliff?”. Everyone was standing up and those who thought ‘more than’ would put their hands on their heads, ‘less than’ on their waist. If you guessed wrong you sat down, if you got it right you remained standing. Cue a few more rounds of this and the last three people standing won prizes. Neat group game and a perfect way to warm up for the day.

More than or Less than game. Photo by Em Bell on twitter.

Workshop 1 : Reviving and Rethinking the Structured Variation Grid

Delivered by Jonathan Hall (aka mathsbot – shameless plug to his site as I am a Patreon) his workshop launched this brand new resource on the site. He mentioned the origin of this variation grid by Anne Watson and John Mason. And an original flash based app with the same purpose.

Jonathan Hall on Structured variation grids

He showed us the original idea of ‘going with the grain’ and ‘against the grain’ both horizontally and vertically on a structured grid (spreadsheet like cells). Where the task changes just a little on each cell in line with variation theory. This is such a neat idea and hones into the human instinct of pattern prediction and filling in missing information (like crosswords for example). I would encourage to explore his site and the grids.

Digital versions available on the mathsbot site

Workshop 2 : Don’t Stop Interweavin’ (Hold On to That Feelin’)

For me this was the best title for a mathsconf presentation, ever. And it just goes to show how you can bring our own personality into a mathsconf workshop. Playing into his jovial style of punnage, maths history and very well thought out tasks (which don’t shy from challenge and a lot of practice), Nathan Day opened this session with a call and response singalong. To the very title of this workshop with the melody of the Journey song. I was all in.

Nathan Day with a call and response to “Don’t stop interweavin’ (hold on to that feelin’)”

Nathan runs the excellent website interwovenmaths.com which does exactly what it says on the tin. Connecting different areas of maths up into intelligent tasks. For example, I was covering the fraction operations with a Year 8 tutee, who was then covering linear sequences at school and wanted help with that too. So I interweaved the two and did fractional linear sequences, with negative numbers thrown in for bonus. This is the general idea behind interweaving.

Exam questions like Hannah’s sweets interweave topics anyway to test thinking flexibly and the ability to cross connect ideas in different areas. Very important for young mathematicians in developing problem solving skills. The interweaving does not have to fit the real world. We got to see some SURD money examples, money can be irrational as well.

We got to brainstorm and create our own intervowen questions as well, tasks at the heart of the workshop. Interweaving should be carefully considered, not just done for the sake of it, appropriate to where pupils are in their mathematical development and tasks should be cognitively demanding.

Money is irrational, something we know already, but in this case it was quite literal!

For more details, Nathan has not only released the full presentation PDF but there’s detailed commentary on this twitter thread. Do check it out and explore the website for tasks.

Workshop 3 : Conceptual Maths

Calculation isn’t the important bit

This quote was on nearly every slide and summed up such an important idea behind being a mathematician. Calculation (to get some sort of final answer) is not the most important bit.

Pete Mattock on Coceptual Maths. Photo by @Noni_Rainbow on twitter

This workshop by Pete Mattock was on his 40th birthday. Choosing the day to present and share his knowledge to fellow teachers. Not only that but the colours of the slides were of the Ukrainian flag in solidarity with the nation.

Pete went straight into busting BIDMAS/PEMDAS etc. followed by some neat tasks on the distributive field axiom (distributive property of multiplication over addition).

We then moved on to Trigonometry with the wider context of similar shapes in triangles. There were some neat tasks for those as well.

Pete will be releasing a book with the same title ‘Conceptual Maths’ and his YouTube channel is well worth checking out. I cannot wait to host him for more episodes of #MathsChatLive and keep the conversations going.

Workshop 4 : All Things Being Equal: The Life and Times of Robert Recorde

This was the first time I went to a workshop by Gareth Evans. For those who know me, I am a little obsessed over the equals sign. All my tutees get to hear the story of the origin of that sign from Robert Recorde’s quote in his book.

Welsh terms by Recorde

But I did not have a more in depth history of Recorde’s life and the context in which he existed. It is no exaggeration to say that by writing the first ever English language books of mathematics, he played a huge part in shaping the type of mathematics symbolism familiar to us today. He was as Emma Bell says in her blog, a trailblazer.

The hand symbols used to represent numbers by the traders in the Welsh docks was pretty cool. For me (and the rest of the room), the symbol of 4 (the rock symbol or the devil’s horns \m/) was a an amusing moment.

The first asynchronous maths tutoring ever in English, by Robert Recorde

Recorde’s life, along with his books and the era in which he existed was narrated beautifully. While La Salle have come up with TUTOR, it was really Robert Recorde who came up with the first form of scaleable remote tutoring with a master and scholar type narrative in his books. With lots of amusing story like language in them, at times even berating his imaginary tutee!

We also saw a neat multiplication algorithm that requires pupils to know just the multiplication facts of up to 5 x 5. That used to suffice in those times. To work out the rest of the multiplication facts (up to 9 x 9), the algorithm and its proof make for some great mathematics. (Video and more detailed method coming up here later – for now check out this tweet)

Workshop 5 : Old Yellow Bricks: Developing an Evidence Informed Approach to Concrete Resources in the Mathematics Classroom

I am a big fan of Kieran Mackle’s podcast (+ book) ‘Thinking Deeply About Primary mathematics‘ and the Discord community he has set up. Primary mathematics is the absolute bedrock of the subject and I am so glad that more primary practitioners are running workshops at mathsconfs. I hope to see even more in the future.

Kieran Mackle on the ‘less is more’ aspect of using manipulatives

I use manipulatives and multiple representations regularly, so this workshop was going to be totally up my street. Using manipulatives always comes with a health warning and for all the right reasons. Their use is not as straightforward and should be carefully considered as to how they will bridge from pupils’ current understanding to bring about new knowledge. Now I’ve always felt that to be the case but what Kieran did was to evidence that with some well referenced papers and studies. And one of the quotes that “meaning is constructed with, not by the manipulatives” was a great reminder.

Great summary on the various moving parts involved in teaching with manipulatives

Kieran also ran a Jamboard exercise where he got delegates to move blocks and virtual cuisenaire rods on their own jamboard slide using their mobile phones. Instant group feedback and interaction appearing live on the presentation itself. Very neat indeed!

I definitely encourage teachers to use manipulatives. Their effectiveness can only be experienced by teaching. Only by testing, tweaking, adjusting and refining how you use them in the real world will you get the feedback and feel to understand them. There is also a great community of teachers you can check in and get support from. Along with blogs of teachers learning how to use them.

Final thoughts

When Mark McCourt was on #MathsChatLive earlier this month, he remarked that of all the things he has done in the last ten years, mathsconf was what he was most proud of. And for good reason. It’s an incredible community that attracts those who love teaching mathematics, a place where I feel at home. When teachers go back to their daily teaching from a mathsconf and apply new ideas, they are impacting thousands of pupils straightaway, and even more in the long run.

A huge thanks to Mark McCourt and the entire La Salle team for making the magic happen

Like everyone else I was limited to just 5 workshops on the day while missing many other great ones. It was suggested that workshops should also be streamed live and recorded. But being a streaming geek myself, I know how complex it would be to stream an entire in-person conference. It would require a lot more hardware and a production team. There are easier options like recording just audio and listening later with the PowerPoint presentations that delegates already receive. I’m sure in time the conferences will evolve naturally to cater for this as the recordings are absolutely invaluable.

Meeting Rhiannon Rainbow in person again, both wearing black and white stripes!

On a final note, the conversations around #MathsConf28 will continue to reverberate. And I definitely want to play a role in this. So if you ran a workshop and want to discuss it more, do DM on twitter or email. I am always looking for panelists, following the La Salle ethos that anyone teaching maths in any capacity should share and articulate their ideas. We are intellectuals, we have theories and we need to learn from each other.

See you at #MathsConf29, Kettering here we come.

The smiles say it all. Maths teaching colleagues in fine company with each other

Teaching with multi-base : Escaping my own base-ten world first

Leave a Reply

Fish don’t know they’re in water. If you tried to explain it, they’d say, “Water? What’s water?” They’re so surrounded by it that it’s impossible to see. They can’t see it until they jump outside of it.

Derek Sivers

Sitting in a park in central London on a warm, sunny June 2018 day I knew something in me had shifted forever. My head was full of swirling mathematical thoughts processing just what had happened during those last hours. Before this day, I had no interest in working with multi-base. It seemed impractical and if I am honest, an unnecessary indulgence. But something in my brain was broken and unresolved after I was unable to do an exercise at that CPD workshop. And I had to get to the bottom of it. So I began a journey of curiosity, frustration and wonder into the world of multi-base.

That CPD day was delivered by La Salle Education CEO Mark McCourt and was titled “Making Maths Memorable”. I had learnt many things that day, including the split attention effect, non-examples and the careful use of silence when presenting visual information. The workshop wasn’t a multi-base workshop as such but it had clearly piqued my interest. Over the years I started adapting ideas from the workshop to my seemingly alien world of online tutoring. My teaching was to be transformed.

It took me several months to do anything with multi-base after that workshop, perhaps because I had no starting point or representation to grip the idea. Until I heard about numbers, numerals and digits in a podcast by Mark again. It turned out I didn’t know abut this either. How could I convey these early, basic ideas to my tutees if I didn’t understand them myself? There was a big, gaping blind spot in my teaching staring back right at me. It existed because none of these things are tested in the current English maths curriculum or any of the other systems I had encountered. And I’ve tutored in over 25 countries! So if it isn’t tested for in any curriculum then is it worth learning?

Well obviously yes, because mathematicians are curious and seek enlightenment. I knew that understanding number in depth held an important key, not just for my lowest attaining pupils, who I felt would benefit most from the knowledge at first, but for all pupils. I looked up various definitions and started exploring the world of numbers. Having grown up in Libya and India I was already familiar with modern Eastern Arabic numerals and Hindi Devanagari numerals.

If you want to master something, teach it. A great way to learn is to teach.

Richard Feynman

I found a Year 7 tutee to test my ideas and understanding with multi-base. I had tutored her since Year 5 and her parents were open minded on my teaching of ideas beyond the curriculum. She was a diligent, curios and bubbly learner. She was honest and clear live when teaching : “I don’t get this”, “What do you mean when you say numeral?” etc., This batting to and fro was what I needed to tweak and refine my delivery in real-time. This is a fairly routine aspect of tutoring, a conversation and constant running of experiments to gauge where the tutee is at.

With my help she made an odometer type counter on our digital writing platform Bitpaper by programming the numerals in steps of 1. Pressing the forward or rewind button (Undo and Redo) would get the odometer to count up or down in various bases. Much like the counter of fuel at a petrol station does in base-ten. An odometer counting up is all I could think of and I didn’t come back to multi-base again for a few more months. Unknown to me there was a bigger issue I had to resolve first.

An immediate problem I faced was that the number system in base-ten was so deeply ingrained in my mental programming that it was difficult to think outside of it. Whenever I saw 14 written in various bases, I read and saw it as fourteen. I needed numerals from another language altogether to break the association of base-ten with the way digits are combined to make everyday numerals. I found the perfect bridge both for me and tutee by using Hindi (or Devanagari) numerals.

It is somewhat embarrassing to admit that despite having grown up in Libya, Yemen and India, I had no idea that the modern numerals we use today are Hindu-Arabic numerals. It is never too late to learn of course and it sure makes for good stories with tutees. Incidentally, Libya has a lot of Roman monuments preserved immaculately, so I was surrounded by a blend of ancient Roman numerals, Hindi numerals and Eastern Arabic numerals during my childhood days in Tripoli. It felt amazing to look back at something so familiar and find deeper meaning through these numerals.

Base-three Diene blocks from my set.

Over the next two years I attended various other La Salle CPD days in London on multiple representations. Each one had a mention of numbers, digits and numerals and counting in different bases. I read books, found videos and podcasts too. I started to see how the area model could be used to understand number systems in other bases. In particular the use of Dienes blocks which Zoltan Dienes used in various other bases. I even got hold of an incomplete set of physical wooden sets of multi-base blocks, which looked very cool. My understanding was starting to deepen, but I didn’t feel confident enough to start teaching with virtual multi-base blocks, the only ones I could use online with my tutees. Base-ten blocks were no problem at all and I was using them before anywyay.

In all this time, I started to fine tune my skills in teaching through various representations. Particularly the use of the Rekenrek, algebra tiles, Cuisenaire rods and two sided counters. After seeing a back to back session on the use of two sided counters by Jonathan Hall (aka mathsbot) and Bernie Westacott, I started to realise how incredibly effective two sided counters could be for teaching so many mathematical ideas.

Fast forward to March 2020; a global pandemic happened and life turned upside down. I was fortunate that I kept tutoring online as I had done for all these years and that time was well spent in exploring virtual manipulatives to teach students in far flung corners of the globe. This experience of operating in the virtual 2-D world of online tutoring was about to pay dividends in how I could understand and teach multi-base. Not just to my tutees but as CPD later, both receiving and delivering it.

#MathsConf23, like many events, went virtual a few weeks into pandemic. The “Explode your mind with exploding dots: A global phenomenon” presentation was given by James Tanton who radiated a teaching life force and infectious enthusiasm. By then I had already been using dots/counters/rekenreks, so I got this representation immediately. For the first time, multi-base started to make clear sense and a whole new universe revealed itself to me. I was breaking out of the shackles of base-ten.

I then started helping my tutees prize this association apart. Disrupting someone’s worldview is no easy task but my tutees trust me. Besides, younger tutees had not lived with base-ten for as long as I had, so they were fairly quick to grip multi-base. Nonetheless, I took an incredible amount of care and caution to make sure that tutees do not get muddled up. Always starting from an open ended exploration of numbers, digits and numerals before presenting clear cut definitions. Regularly reminding them that a numeral is the written code and representation of number, whereas number is the thing itself, the idea.

Once familiar with binary with Hindu-Arabic numerals, I encourage tutees to make up their own digit symbols. Here we have a comb (one) and pumpkin (zero) from a tutee.

I sidestepped working in multi-base with Hindu-Arabic numerals with my tutees and started using a mix of ancient Egyptian and Roman numerals first. Roman numerals turned out to be a great bridge into this world for my tutees as they were already familiar with them. And in this last academic year, I have thoroughly explored exploding dots as my go to representation for multi-base, both with whole numbers and whole + fractional numbers.

I have now emerged on to the other side; now when I see 14, I see a numeral that is one-four. A symbol that could represent various other numbers depending on base choice. I even get the joke: “There are 10 types of people in this world, those who understand binary and those who don’t”! And since September 2020 I have been covering a range of multi-base ideas with tutees, from long addition algorithms to division. It is only a few months on but I am already seeing them develop robust and flexible generalising skills. They are becoming more mathematical and some of them are already comfortable working in base-x.

I have a lot more to write about teaching multi-base and will do so in a series of blog posts, particularly on the idea of place value. Once you are enlightened about place value, it is impossible to teach place value in just base-ten. Because teaching it in just base-ten does not feel like teaching place value at all. Education and CPD is the way out of this, just like it has been for me. Place value in other bases has also been mentioned by Charlotte on her blog post and there are some really great definitions of various related ideas on Mark’s blog post too.

Exploring ancient Egyptian numerals. A task my tutees do and one I set for my #MathsConf25 workshop.

So how to get started on multi-base (radix)? You can of course look it up online, in various books or take CPD. The exploding dots website is a great place to get started on it. I presented a workshop at #MathsConf25 titled “An introduction to Multi-base” which was specifically designed for complete novices with my fresh viewpoint. I really encourage maths teachers, tutors and pupils to explore the world of multi-base. There is something profound missing if you don’t understand it.

Disrupting one’s own existing worldview and frame of reference is no easy process. But as teachers we know this better than anyone else. An incredible journey awaits for you if you haven’t explored this world yet and want to dive into it.

Decimal Day : 50th anniversary and multi-base

Leave a Reply

“It is estimated that up to six months will be saved in teaching time by the introduction of decimal money”

British Pathe news video clip – ‘Decimalisation (1970)’

On 15th February 1971 Britain changed forever and day to day life would never be the same again. The monetary system went from mixed-base (‘old money’) to base-ten or decimal (‘new money’). Decimal Day ended a run of over 1000 years of a mixed-base money system.

Deci comes from Latin ‘Decimus’ (tenth), which is closely linked to Decem’ (ten). By switching to a base-ten currency, 100 new pence became equal to 1 pound sterling. Gone were all the other exchanges.

The history of the pound sterling goes back to the Romans. The £ symbol is an ornate version of L, for libra, worth one pound mass of silver. Libra is abbreviated as lb which we still use to measure weights. The shilling (s) came from a type of Roman coin called the solidus and the penny was abbreviated with its Latin name denarius (d).

So the old system was abbreviated as £sd (or Lsd for librum, solidus, denarius) or LSD for those groovy 1960s times. The main exchanges were:

1 pound = 20 shillings
1 shilling = 12 (old) pennies

Other coins in use were:

2 farthings = 1 halfpenny
2 halfpence = 1 penny (1d)
3 pence = 1 thruppence (3d)
6 pence = 1 sixpence (a ‘tanner’) (6d)
12 pence = 1 shilling (a bob) (1s)
2 shillings = 1 florin ( a ‘two bob bit’) (2s)
2 shillings and 6 pence = 1 half crown (2s 6d)
5 shillings = 1 Crown (5s)

Although the preparation had been going on for years the currency transition was tricky. Prices were initially shown both in old and new forms. People had to get used to the new pence and other new coins. There were many benefits proposed by the government for going decimal, from reducing teaching time at schools to the use of fewer accountants for businesses.

Even though our monetary system was decimalised all that time back we use mixed-base every day today. Time.

1000 milliseconds to one second (base-ten)
60 seconds to 1 minute (base-sixty)
60 minutes to 1 hour (base-sixty)
12 hous or 24 hour clock

And these days pupils have to understand binary and hex numbers for use in computing.

50 years ago is not that far back and there are many adults who will remember Decimal Day. If you were one of them, I would love to hear your experience of it all. So do drop a comment here on this blog post.

Delivering my first maths conference workshop #MathsConf24

4 Replies

Just over 3 years ago I attended my first ever maths conference #MathsConf10 in London. That event was to change the course of my teaching life forever. I plugged into a network of passionate maths teachers and went deep down the rabbit hole of CPD; from books, articles, journals, CPD videos, podcasts, twitter discussions, conferences, the La Salle CPD days, webinars to hosting #MathsChatLives and more. Back in June 2017 I could not have dreamt that I would one day be presenting at a MathsConf. I felt so out of place even amongst tutors since I was the oddball one teaching entirely online. None of that mattered once I plugged into a network where everyone had the love of teaching maths in common.

I attended the mathsconfs religiously over the last 3 years and got to know the regulars. With the La Salle CPD days I started finding parallels with my previous experiences of CPD in industry and in academia. I knew that presenting to peers is an important aspect of professional self development, personal growth and accountability. Imperial College had a great ethos of communicating Science and I had already presented at Tribology conferences, both in poster and presentation format. That journey ended for me in 2005 however when I left university academia. So to go back to powerpoint after all these years was a daunting and exciting prospect.

When #MathsConf23 went virtual, it was brand new territory and I was prompted to put in a workshop proposal. I had run some live online CPD courses on Zoom for tutors before (Indie Tutors) and of course #MathsChatLive but that was very different to a full maths CPD workshop. I was both excited and nervous at the prospect of presenting a workshop. Excited, because the virtual teaching environment is now my natural teaching environment. Nervous, because of imposter syndrome! All my teaching is one on one and therefore I rarely ever talk for more than 5 mins before interacting live with a tutee. So I didn’t have the nerve to put in a proposal for #MathsConf23 where I’d be talking for an hour. Instead, I took the smaller steps of presenting for 5 mins first to the #LockdownStaffRoom group of maths teachers, then at the Seneca maths conference, and then as a panelist on the Tutors’ Association webinar. I gained more confidence after these short presentations. So finally, I submitted #MathsConf24 proposal for a full one hour presentation.

But what would I present on? I didn’t want to talk about online tutoring like I had done for the mini talks. Instead, I wanted to focus on specific aspects of mathematics teaching itself. I had 14 years of teaching behind me and felt that I should cover things I have learnt in all these years. The imposter syndrome inner voice said “you have nothing new to add, everything you have to say has been said before and what if the stuff you are saying is wrong?” and the other voice said “that might be true but every teacher interprets and executes the teaching of the same idea in a unique way, and therefore what you have to add to the canon of knowledge will be valuable to someone. And you now have accountability from your peers. This is the opportunity and feedback you have been waiting for all these years”.

I decided to present on how to help the lowest attaining pupils. The ones that have made me totally rethink how I teach. And have made me a more patient and understanding human being. In the last 3 years I have learnt a lot about using multiple representations which has been an eye opening and exciting journey. This quest to help my pupils has sent me down the path of learning how to teach the very earliest of maths ideas. I had to learn to teach everything from skip counting, number bonds to the meaning of “fraction-ness” and so much more. And this was hard, really hard. The earlier the maths idea or concept, paradoxically, the harder it seemed to be able to teach it well to someone who didn’t grip it. I had never thought about what a number means. Or what the difference is between numbers, numerals or digits. But once I started understanding these concepts more (thanks to CPD), I was also able to help my pupils make meaning of it. I felt enlightened in a way I had never before. And this journey is what I wanted to share. Along with practical ideas of course. The engineer’s mindset has never left me, practical, pragmatic actions that yield results. Some that I had hacked up along as a result of CPD and real world implementation.

So I started preparing my presentation. After a little battle with Powerpoint, I thought I’d try out Google Slides instead. I just couldn’t do it as I couldn’t figure an easy way of writing live on my presentation using a digital pen or to move manipulatives about on either PowerPoint or Slides. After some consideration I decided to use BitPaper for the presentation itself. BitPaper is not a presentation software as it has only one font and no option for any text formatting other than changing size and colour. But that was enough for me. And in some ways I found that restriction quite liberating with such limited choice.

The more I prepared it, the more I realised that my presentation will resemble my day to day teaching canvas itself. This gave me a great sense of relief, as snippets of my day to day online maths tutoring, from content relevant to primary teaching, secondary, GCSE etc. was what I wanted to share. I even started to copy and paste actual teaching examples from tutoring sessions into my presentation. Planning a whole hour teaching session was also something new I had to learn. And if I am honest I have never prepared a one hour lesson in my life ever, as it is not needed in tutoring. But I had prepared research presentations before, so that was the frame I was taking. Still, I just couldn’t run a presentation with any live and real interaction, so I put my thinking cap on to design elements of this. I had seen some La Salle CPD webinars that had neat interactivity with chats and polls, so that stimulated me for more ideas.

I started putting little snippets of text as ideas on the notes app of my phone and then to the presentation file itself. Every time I got an idea I felt I wanted to present I’d make a short note of it. Like so many teachers/tutors I’ve had the busiest of terms ever in my teaching career so far and I didn’t get a good enough stretch of time to work properly on the presentation. Two weeks before the big day arrived, I barely even had a slide ready. The publicity for the conference was going full steam ahead by then and my workshop would occasionally be plugged.

It was time for me to knuckle down and deliver. I started throwing all my ideas down now. At first I thought I wouldn’t have enough material for a full hour talk. But it was clear that if anything, I now had too much material with one week to go before the workshop. So I now started trimming some ideas down. A couple of teachers on twitter also tweeted they had cut their presentations down so I knew I was on the right track.

In fact I was still finalising slides the night before the conference and I was still feeling bogged down by it all. I had not even done a run through of the talk to see if it ran on time. Though I did a technical check with my tutor colleague Paul the evening before. What helped tremendously was being on a live zoom group social call in the #LockdownStaffRoom with some of the maths teachers I’ve got to know so well, including my La Salle presentation host being there as well. The company of other maths teachers face to face virtually made the finalising of slides such a pleasurable and motivating experience. I realised that I’m presenting to colleagues, who just like me live and breathe maths teaching. And have taken a day off from their busy lives to present and be part of the conference. This breathed new life into me and I finished the whole presentation off. I did one last test run after the #LockdownStaffRoom social. The presentation ran to 50mins, plenty of time to spare for the real thing. I had built in some real time interaction with the audience as well using twitter, which I was really glad about. But would this actually work out on the day?

My presentation was in the first period for 9:30 am out of the six on the day. I was mightily happy about the prospect of getting it out of the way first thing and not feeling nervous all day instead. I did some pre flight checks on all my tech; microphone level, camera image and lighting, screenshare window of presentation, chat window with La Salle, chat window with audience and twitter browser tab. All ready to go.

With great energy my host Jonny Hall aka mathsbot introduced me and I started it all off by welcoming everyone to the mathsconf and thanking everyone for taking time off on their weekend to hear me live. After about 5 seconds of nerves right at the very start I was in the flow of it all. Like a teaching session with a tutee it flowed very smoothly and I was well into my element. From performing as a musician I know when a singer records in the sterile and lonely environment of a studio they have to put themselves in the headspace of singing that song to just one person. Live at a venue is different and the energy for the same song needs to be dialled up to fill the room. So in my head I was presenting to just one person, the delegate on the other side of the screen. This made me feel more relaxed as well as I wanted every delegate to feel that I was talking to them individually on their side of the screen. Just like I do in my day to day tutoring.

The audience chat was very useful to keep an eye on as I got to know which ideas were resonating and leading to peer to peer discussions. I asked some questions on ideas behind numbers to get everyone thinking and was delighted to see answers coming. The exercise that I really wanted to test on on scale using twitter was one based on the use of Egyptian Hieratic numerals as part of the sections on numerosity (numberness), numbers, digits and numerals. This is one of my absolute favorite exercises that I do nearly with all my tutees of any age. It is one thing doing these with tutees so I was curious to know how it would play out with fellow teachers. As part of the section on numbers, digits, numerals, I went to explaining how the numberness of a number can be drawn out using Egyptian Hieratic symbols live using an example. I asked delegates to draw their own versions out, take a picture of that on their smartphone and post it live to twitter.

#MathsConf24 Live interaction of delegates’ handwritten exercises in real time.

There was a 20 second delay in the live video being streamed to delegates so I had to wait a little and not talk at all during this short time window. I initially made the mistake of switching to the twitter tab too fast and not giving enough time for delegates to see the screen. The chat window feedback was instant. I corrected and went back to the slide with the task and stayed on it. After about a minute, something beautiful happened. My twitter timeline was flooded with answers. Handwritten with pen and paper. Each one with its own unique personality. There was something really human and organic seeing delegates handwriting appear in real time. I took two of those examples from twitter and snip-pasted them live into my presentation. So two of my delegates now became part of the presentation! My gamble had paid off and I felt real connection with delegates from that point onwards. It was now two way real time communication.

I went through a bunch of things on the presentation, sometimes writing out explanations using my digital pen, moving virtual manipulatives and of course talking in the context of the slides. The presentation itself would be a blog post of its own but for anyone interested, the video recording is available to buy as part of the La Salle Teacher CPD college #MathsConf24. I concluded my presentation, looked at chat questions and answered as many as I could. Jonny Hall my host also asked a question on behalf of a delegate and we had a little bit of a chat at the end. And then I wrapped it all up. Phew, that was a good one and I was glad that was out. Onwards to taking part in the rest of the conference which was so stimulating.

So my first workshop was fourteen years in the making. I would possibly be the first career tutor to present at a conference like this. Hopefully paving the way for many other of my tutor colleagues who I know are also keen to present. I really recommend tutors to take the plunge as La Salle are really open minded with these things. A few other teachers also made their debut for a maths conference presentation so I wasn’t alone. I have much still to learn about teaching mathematics. So being able to share whatever I have learnt so far with my peers is a superb opportunity. The beginning of a journey of accountability, enthusiasm, personal and professional growth.

Being Featured on the Wall Street Journal as a live-streamer

Leave a Reply

In the middle of my short holiday at the Peak District an article appeared on the famous US newspaper on the 6th of August 2020. The article was titled ‘Everybody Is a Live-Streamer in Covid-19 Era‘ and I featured on the opening paragraph for that story. The article was published in print of the Wall Street Journal as well.

“Soon after the coronavirus outbreak was declared a global pandemic, Atul Rana started using the video app Zoom to keep up with peers in his field. The high-school math tutor found the hourlong conversations so enlightening, he began broadcasting them live once a week on Twitter, Facebook and YouTube.”

Sarah E Needleman – Wall Street Journal, 6th August 2020
Print version of Wall Street Journal article ‘Look Who’s Live-streaming’, Atul Rana is 🙂

I had been contacted by author Sarah earlier and this seemed like a pretty cool story to be part of. Little did I know that I was a part of a new type of media creator in a family of live-streamers, a niche of sorts, people who stream about fitness training, video games, music and more. Which in itself has given me more ideas to try out for other things I do.

Maths Chat Live Stream with Atul Rana hosting on zoom
#MathsChatLive Stream hosted by Atul Rana and broadcast on twitter, Facebook and YouTube.

I already mentioned in a previous post that one of the highest leverage activities I thought I could engage in as soon as the Covid-19 pandemic went global was to live stream with UK based maths teachers. I was an early adopter to live streaming, starting from streaming live music gigs in my room from 2014 on YouTube, to 2016 on Facebook, to education live streaming on my Facebook Page and eventually Indie Tutors to help other tutors.

The need for a community of passionate maths teachers to communicate and share their thoughts has always been there. And there is a really rich and diverse community of UK maths teachers and tutors on twitter. The pandemic brought to an end of face to face conferences and meetups for a few months. I felt that loss as well. I felt I had to now rise up to a new role. To bring my expertise as an online maths and science tutor in holding an online space for tutees, to now holding it for these passionate maths teachers and to learn from them.

Unlike the earlier live streams, these were multi streamed simultaneously on twitter, Facebook and YouTube. I invented a new way of maths CPD online as more and more people gave me ideas. One great idea was to take questions live on twitter and discuss them on a panel.

Anyway, enough of my self congratulatory post here 🙂 I really like the idea that now anyone can run their own TV show online, not just mainstream or any other media. And over the coming months I hope to train up others to livestream like I do using OBS, restream and social media, so this becomes more of the norm and a new thing.

Interactive Virtual Manipulatives in Online Chemistry Teaching – Creating Molecules

Leave a Reply

Over the last 2 years I have been mentoring Paul Morgan, an A Level Chemistry tutor on his move to tutoring Chemistry online. With Paul being based in Burnley and me in London, we are still yet to meet in person. We have been meeting on a video call every week which serves as part staffroom and part CPD. We discuss a range of things from the business side of tutoring, teaching techniques online and more recently I have been his test pupil for the Chemistry teaching videos he records while we are on a call. So in effect we are on a video call, an interactive canvas and online video recording studio.

I teach up to GCSE Chemistry and Paul being an A Level Chemistry specialist, I have learnt a lot from him. Particularly how what I am doing at GCSE and earlier stages links up with what comes up at A level. Always keeping a long term view of learning Chemistry and making sure that things are taught correctly the first time round in the learning journey. I did A Level Chemistry and did research in a multi-disciplinary Tribology lab at Imperial College. So Chemistry has always been of interest to me.

One of the great things about using interactive online whiteboard Bitpaper (disclaimer : I work for them as their social media rep) is that you can build a whole bunch of filled shapes. Both the tutor and tutee can move these shapes around. For maths teaching this has been excellent since I have made my own two coloured counters, algebra tiles and cuisenaire rods. A tutee can be thousands of miles away from me yet both tutor and tutee can move the manipulatives around on screen as if we they were on the same table.

The use of interactive virtual manipulatives on Bitpaper to show how atoms are arranged to form molecules.

I have started to use virtual counters in teaching Chemistry as well now. In Chemistry students may use ball and stick manipulatives at school to understand the basic formation of molecules, the relative arrangement of atoms in space in that molecule, bond breaking and bond breaking etc. Quite a lot of that movement and playing with things can be replicated online.

We have created a series of videos to show exactly this. This first video is the very first one that introduces virtual manipulatives. Some things to note:

  • The atoms sizes are relatively in proportion to each other approximately.
  • The subscript symbolism of what the molecule represents with a pictorial representation of the molecule needs to be explicitly practiced by students.
  • Embedding what monoatomic and diatomic means using a pictorial representation.
  • Common misconceptions are addressed using non-examples. For example, while Methane’s molecular formula is written with Carbon first and Hydrogen with a subscript of 4, that does not mean that the molecular representation has a carbon atom, followed by four Hydrogen ones in a row.
  • The whole process of forming a molecule from atoms is then animated by the tutee once they have manually formed the molecules. This is done while I keep silence. Silence from the tutor is key to reduce cognitive load on the tutees while they discover and make these molecules.

I have tested this with a number of pupils now online and Paul has started using it with his tutees as well. It has been really useful for me to consult Paul and together we are creating this new way of working with manipulatives for Chemistry when teaching online. Please do let us know in comments or on twitter/Facebook what you think of this.